Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 02. 2015 20:18
Výpočet vzdálenosti dvou bodů
Dobrý večer,
nevěděl by někdo, jak na tento příklad:
Na přímce AB, kde A [-3; 2], B [2; -3] určete bod M tak, aby platilo ǀAMǀ = 2/3*ǀBMǀ
Jde o příklad z Petákové.
Zkoušel jsem si pro M dosadit X a Y do ǀAMǀ = 2/3*ǀBMǀ a vyšla mi ošklivá rovnice o dvou neznámých, na které jsem skončil. Ještě mě napadlo udělat si z toho obecnou rovnici a tu dosadit do toho vzorce a tím mít jen jednu neznámou. Tím mi vznikne ještě něco ošklivější a po prokousání se tím stejně končím na něčem, co nedokážu vyřešit. Máte někdo nějaké nápady?
Díky moc :-)
Offline
- (téma jako vyřešené označil(a) vachyto)
#2 10. 02. 2015 21:06
Re: Výpočet vzdálenosti dvou bodů
↑ vachyto:
Dobrý den.
Úsečku AB lze snadno rozdělit bodem M v návaznosti na dělící poměr 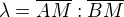
(pozor, úsečky AM, BM jsou orientované úsečky):
Dáno: 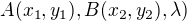
Pak bod M má souřadnice: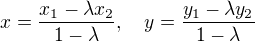
Řekl bych, že pro daný příklad bude 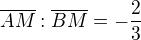
(úsečky AM, BM jsou opačně orientované --> lambda < 0)
Takže: 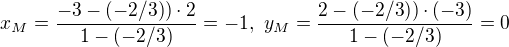
Poznámky:
- pro půlící bod úsečky je lambda = -1,
- vztahy pro x, y jsou rovnicí přímky dané dvěma body a proměnným dělícím poměrem.
Pokud se tedy nemýlím.
Offline
#3 10. 02. 2015 21:16
Re: Výpočet vzdálenosti dvou bodů
↑ Jj:To vypadá nad míru dobře a s výsledky se to shoduje. Ve výsledcích je ještě M2 [-13; 12]. Dá se na to přijít nějakou podobnou metodou? Nebo je způsob řešení úplně jiný? Každopádně Vám patří veliké díky
Offline
#4 10. 02. 2015 21:17 Příspěvek uživatele Darko byl skryt uživatelem Darko. Důvod: špatně jsem přečetl zadání
#5 10. 02. 2015 21:34
Re: Výpočet vzdálenosti dvou bodů
↑ vachyto:
Aha - já jsem si nějak vsugeroval, že jde o dělení úsečky - ovšem jde o poměr vzdáleností. To by mělo mít ještě jedno řešení, kdy bod M leží vlevo před počátečním bodem A úsečky AB. Pak bych to viděl na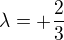 (AM, BM mají stejnou orientaci).
(AM, BM mají stejnou orientaci).
Pokud se tedy nemýlím.
Offline
