Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 03. 2015 20:05 — Editoval Vladislav97 (27. 03. 2015 20:07)
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Logaritmické rovnice
Dobrý den,
mám potíž s příkladem, který má neznámou v základu logaritmu. Krom toho, levá strana rovnice je v součinu a všechny základy logaritmů jsou jiné.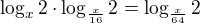
Zkoušel jsem všechno možné. (např upravit logaritmy na podíl se stejnými základy):
např. ten první člen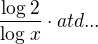
anebo: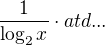
ale do žádnýho vhodnýho tvaru. kde bych se mohl zbavit logaritmu a porovnávat jenom ty argumenty, jsem nedošel.
Prosím o pomoc. Děkuji.
Offline
- (téma jako vyřešené označil(a) Vladislav97)
#3 27. 03. 2015 20:22
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Logaritmické rovnice
Zdravím,
došel jsem sem: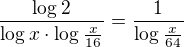
Offline
#5 27. 03. 2015 20:41 — Editoval Vladislav97 (27. 03. 2015 20:43)
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Logaritmické rovnice
[re]p470114
Moc nechápu jak...všechno má přeci stejný základ.
Ledaže bych se to pokusil napsat jako rozdíl logaritmu.
Offline
#6 27. 03. 2015 20:44 — Editoval Vladislav97 (27. 03. 2015 20:45)
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Logaritmické rovnice
 Takhle by to šlo?
Takhle by to šlo?
A substituci...
Offline
#7 27. 03. 2015 20:58
Re: Logaritmické rovnice
↑ Vladislav97:
Ano, to je možná cesta. Důvod, proč se mi nelíbí, je větší množství iracionálních čísel při následných úpravách. Ale to je jen na tobě, pokud se tím chceš prokousávat. Doporučil bych celou rovnici ještě vydělit číslem 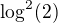 , tím dostaneme
, tím dostaneme ,
,
tj.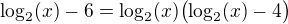
což je o poznání příjemnější.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#8 27. 03. 2015 21:01
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Logaritmické rovnice
Proč se to dělí 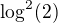 ane
ane  ?
?
Offline
#10 27. 03. 2015 21:17
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Logaritmické rovnice
No, kdybych dělil 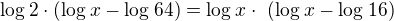 tímto
tímto  , tak asi pak přeci dostal, to co jsi napsal:
, tak asi pak přeci dostal, to co jsi napsal:  Nebo...uniká mi něco?
Nebo...uniká mi něco?
Offline
#12 28. 03. 2015 14:38
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Logaritmické rovnice
Takže: 


To je přeci divný. Vždyť se dělí každý člen...
Offline
#13 28. 03. 2015 17:47 — Editoval misaH (28. 03. 2015 17:54)
- misaH
- Příspěvky: 13460
Re: Logaritmické rovnice
Keď by si delil iba tým log2, netýkalo by sa to vnútra zátvorky.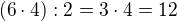 a nie
a nie 
Tým logaritmom sa delí iba raz. Buď delíš to, čo je pred zátvorkou alebo delíš to, čo je v zátvorke. Skús si to s číslami.
Tak aj tým logaritmom.
Offline
#14 28. 03. 2015 18:14
- Vladislav97

- Místo: Praha
- Příspěvky: 421
- Škola: Gymnázium
- Pozice: Student (Druhák)
- Reputace: 13
Re: Logaritmické rovnice
↑ misaH:
Jo, jasný! Nějak mě to zmátlo...teď je mi to jasný, v čem byla moje chyba. Díky :).
Offline
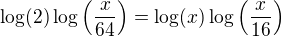 ,
,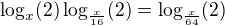
 .
.