Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 05. 2008 13:23
Re: úprava výrazu
ten prvy by som ratal takto: zatvorku spocitas.. vyjde ti ((x^2+x+1)/(x^2)).x = (x^2+x+1)/x
ten druhy .. das na splocneho menovatela, cize ((a+1+a^2+a^3)/(a^2)):((1-a^4)/(a^2)) = ((a+1+a^2+a^3)/(a^2)) . ((a^2)/(1-a^4)) = ((a+1+a^2+a^3)/(a^2)) / (1-a^4) = ((a+1).(a^2+1)) / -((a^2-1)(a^2+1)) skrknes co sa da.. = - (a+1)/((a+1)(a-1)) = - (a-1)
dufam ze som nespravil numericku chybu
Offline
#7 11. 03. 2009 13:08
Re: úprava výrazu
Zdravím,
vůbec si nevím s úpravou jednoho příkladu, který jsem zderivovala a vyšlo mi ´f(x)=cos(3cos(2sin(4x))) krát 3(-sin(2sin(4x))) krát 2(-sin(4x)) krát 4
Jestli to jde nějak upravit, kromě toho že vynásobím jen ty celá čísla 3krát 2 krát 4
Děkuji
Offline
#8 11. 03. 2009 13:33 — Editoval musixx (11. 03. 2009 13:37)
Re: úprava výrazu
↑ Katka1088: Jednak bych doporucil priste zalozit nove vlakno.
Opravdu ti vyslo  ? To se opravdu upravit moc neda. Jakou funkci jsi derivovala? Rozumis derivaci slozene funkce? Tohle ukazuje na to, ze jsi derivovala funkci
? To se opravdu upravit moc neda. Jakou funkci jsi derivovala? Rozumis derivaci slozene funkce? Tohle ukazuje na to, ze jsi derivovala funkci  a na konci mas jeste chybu. Je tomu tak?
a na konci mas jeste chybu. Je tomu tak?
Offline
#10 11. 03. 2009 22:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: úprava výrazu
↑ musixx:
Zdravím :-)
skutečně ↑ Katka1088: derivovala takovou obludu (chtěla bych vidět praktický význam derivování podobného "metodického zázraku") a derivovala dle mého doporučení zde, na závěr tématu: http://forum.matweb.cz/viewtopic.php?id=6583
A když se dopracuješ k obrázkům v odkazu, tak uvidiš názorné pomůcky (наглядные пособия) pro derivování složených funkcí.
Ještě přidám názornou pomůcku pro složené funkce dle definice kolegy Kondra
A srdečné blahoprání k dosažení Einsteina :-)
Offline
#14 12. 03. 2009 09:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: úprava výrazu
↑ musixx:
No jo, samozřejmě bych si troufla, pokud by to ovšem někdo potřeboval (ono tam není níc k troufání, je jen potřeba mít dost čtverečkovaného papíru) - ale necham to ostatním.
Jinak logaritmické derivování je věc zcela nezbytná do života - nevím, zda jsi zaregistroval tuto debatu: http://forum.matweb.cz/viewtopic.php?id=228 - ná závěr debaty Marian dává otázku do debaty - ale pak se to již ukončilo, neboť nám to bylo jasné a nikdo jiný se nezapojil.
Zdravím :-)
Offline
#15 12. 03. 2009 10:41 — Editoval musixx (12. 03. 2009 10:58)
Re: úprava výrazu
↑ jelena: Zajimava diskuze. Prave jsem ji docetl. Ani se nedivim, ze se do ni nezapojila ta puvodni tazatelka. :-) Jinak ja jsem se v tomto ohledu setkal i s nazorem, ze kdyz neco resim v realnem oboru a vim, ze vysledek ma vyjit zase realne, je povoleno "skryte" prejit do komplexni analyzy a vysledek bude dobre, protoze se stejne musi vratit zpet do realneho oboru. Je to asi neco podobneho jako ze obecna kubicka rovnice se tremi realnymi koreny resena primo pomoci Cardanovych vzorcu pouziva druhe odmocniny ze zapornych cisel. Ale zpet k tem logaritmum: samozrejme je ten "skryty" prechod do komplexni analyzy zalozen na tom, ze vztahy pro pocitani s logaritmy v komplexnim oboru jsou jakozto termy identicke se vztahy v realnem oboru (tedy ze treba plati log(ab)=log(a)+log(b), nejde mi o to, ze existuji ruzne vetve logaritmu a logaritmus sam prestava byt jednoznacny - nebudu chtit nikdy vyjadrovat log(x) jako a+bi). Nejsem ale analytik a jen po uvodnich kurzech do komplexni analyzy ji nerozumim natolik, abych treba videl, zda se mi nemuze stat, ze prejdu z jedne vetve logaritmu na druhou, aniz bych to chtel, a dostanu tak sice realny, ale spatny vysledek.
Priklad, jak to myslim: misto  pro derivovani vezmu
pro derivovani vezmu  . Vyjde
. Vyjde  , typicky se zpet
, typicky se zpet  nahradi za
nahradi za  a predpokladejme, ze v
a predpokladejme, ze v  jsme se nejakou upravou zbavili
jsme se nejakou upravou zbavili  . Starat se o kladnost funkce f?
. Starat se o kladnost funkce f?
EDIT: Je mi zcela jasne, ze bys s tou derivaci nemela zadne problemy. Uz se chvili tady na foru pohybuju, abych snad dokazal odhadnout, ci prispevky jsou fundovane a ci zase ne tak moc. :-)
EDIT2: Ta analogie s Cardanovymi vzorci neni uplne cista, protoze ty odmocniny ze zapornych cisel zustanou i ve vysledku. Ale snad bylo jasne, jak to myslim. Mozna lepsi analogie je v historii pred pojmem limita, kdy se "pocitalo" s nekonecne malymi hodnotami jako s normalnimi cisly, ve zlomcich se tyto hodnoty normalne kratily a tim se dosahlo toho, ze se vypocet zacal s "normalnimi" cisly, uprostred se pouzila "nenormalni" cisla, ale skoncilo se zase s "normalnimi" cisly. Tak se treba daly urcit smernice tecen - vlastne to neni nic vic nez formalne korektni limita jdouci k nule. Bez jejiho symbolu je to formale spatne, ale fakticky vlastne dobre (s primhourenyma ocima).
Offline
#19 12. 03. 2009 12:38
- marnes

- Příspěvky: 11227
Re: úprava výrazu
↑ ladulinka:Ano. vytkneme 10 z obou členů v čitateli a pokrátíme se jmenovatelem
Jo. A na začátku vás zdravím.
Offline




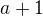 .
.

 ?
?