Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 04. 2015 00:06
Trojný integrál
Dobrý večer všem,
obracím se na vás s prosbou o kontrolu výpočtu tohoto trojného integrálu: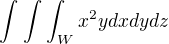 kde oblast
kde oblast 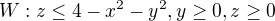
Provedl jsem transformaci do cylindrických souřadnic: 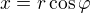
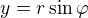

Stanovil meze transformované oblasti: 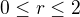
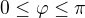
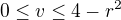
A řešil integrál: 
Můj výsledek 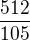 se však neshoduje s výsledkem ve skriptech
se však neshoduje s výsledkem ve skriptech  .
.
Předpokládám, že chyba bude v mém výpočtu, avšak nevím kde.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 06. 04. 2015 10:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Trojný integrál
Zdravím Vás,
mně to vyšlo stejně (před dosazením posledních mezí od 0 do 2 mám  ) , zkuste to vložit i sem bez transformace - také stejně. Jak to vidíte? Děkuji.
) , zkuste to vložit i sem bez transformace - také stejně. Jak to vidíte? Děkuji.
Offline
