Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 04. 2015 18:21 — Editoval smajdalf (10. 04. 2015 18:22)
Počtář Radek - Dirichletův princip
Ahoj všem,
potřeboval bych poradit s jedním příkladem na Dirichletův princip:
16. Radek se připravuje na matematickou olympiádu tak, že po dobu 33 za sebou jdoucích dní vyřeší aspoň jednu úlohu denně. Přitom za kalendářní týden nevyřeší více než 13 úloh. S přípravou začal v pondělí. Dokažte, že pak existuje období několika za sebou jdoucích dní, ve kterém vyřeší přesně 33 úloh. Můžeme vyslovit stejný závěr, když začne s přípravou v pátek?
Díky předem.
"Znám dva tisíce způsobů jak nevyrobit žárovku,
potřeboval bych jeden, aby fungovala."
T. A. Edison
Offline
#2 10. 04. 2015 23:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Počtář Radek - Dirichletův princip
Zdravím,
metody řešení úloh pro přípravu vedení olympiád máš zadávat do které sekce? :-)
Uvažuji, co může počtáři Radkovi překážet každý den řešit pravě 1 úlohu a "období několika za sebou jdoucích dní" mít po celou dobu přípravy (ať začne v pondělí a končí v pátek, nebo jinak)? Jako by tomu zadání ještě něco chybělo. Přesouvám.
---------
"(pokusím se být podrobnější někdy od pondělí do pátku)" (c)
Offline
#3 12. 04. 2015 14:34 — Editoval smajdalf (12. 04. 2015 14:37)
Re: Počtář Radek - Dirichletův princip
↑ jelena:
Já bych to sem dal hned, jenže většina lidí (si myslím) kouká hlavně do těch základních kategorií ZŠ, SŠ, VŠ. Proto jsem to chtěl nejdříve dát tam.
Je to zvláštní příklad, taky mi připadá jako by nám autor neřekl vše, co je třeba.
Edit: I když už jsem, myslím, někde zahlédl dost podobný příklad, ale nevím kde.
No, snad nám tenhle příklad pan doktor do písemky nedá. :-)
"Znám dva tisíce způsobů jak nevyrobit žárovku,
potřeboval bych jeden, aby fungovala."
T. A. Edison
Offline
#4 12. 04. 2015 15:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Počtář Radek - Dirichletův princip
↑ smajdalf:
:-) ohledně "většiny" platí Paretův princip v některé vhodné formulaci. Můžeš analyzovat tempo reakce na Tvá témata (než Tebe najde místní uklizečka, tedy já). Lepší z příprav vedení olympiád dávat sem, jen uvést vhodnou úvodní formulaci ohledně zdroje úlohy a očekávaného předpokladu řešení (tedy metody ZŠ, ale také určitě přivítáš i teoretické odůvodnění i když bude vysoko nad rámec ZŠ).
Jinak obdobnou úlohu jsi zahlédl v některém Tvém tématu, kde jsem dávala stejný odkaz (jen olympionik je Karel a ten má horní omezení počtu úloh). Případně se zeptej pana doktora na kompletnost úlohy. Zdravím.
Offline
#5 12. 04. 2015 16:54 — Editoval vanok (12. 04. 2015 19:33)
Re: Počtář Radek - Dirichletův princip
Pozdravujem,
Navod
Nech 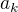 je pocet vyriesenich cviceni v den n° k.
je pocet vyriesenich cviceni v den n° k.
Vieme, ze ( dopln vdaka zadaniu)
( dopln vdaka zadaniu)
Potom ( dopln )
( dopln )
Zvysok' co chyba na riesenie, je ozaj prezakladoskolaka, ktory pochopil Dichlet-ov zasuvkovy princip.
Poznamka: To neznamena, ze dokazes ze dane cvicenie je riesitelne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 13. 04. 2015 21:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Počtář Radek - Dirichletův princip
↑ vanok:
Zdravím a děkuji za příspěvek, obdobné doporučení je i v metodice v odkazu ↑ příspěvek 4:
vanok napsal(a):
Poznamka: To neznamena, ze dokazes ze dane cvicenie je riesitelne.
V tomto případě řešení spíš "nezajímavého rázu", jelikož při 7 až 13 úlohách za týden (+alespoň jedna úloha denně), dotaz bude odpovězen, ale nebude to důkaz.
↑ smajdalf: ověřoval jsi zadání? Děkuji.
Offline
#7 18. 04. 2015 15:44 — Editoval vanok (18. 04. 2015 15:47)
Re: Počtář Radek - Dirichletův princip
Pozdravujem ↑ jelena:,
Tu http://crab.rutgers.edu/~guyk/dmlec/lec … c08/l8.pdf je podobne cvicenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
