Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Problém s důkazem Mittag-Lefflerovy věty (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 04. 2015 22:51 — Editoval Mihulik (25. 04. 2015 22:54)
Problém s důkazem Mittag-Lefflerovy věty
Ahoj,
při procházení Rudinovy knihy Analýza v reálném a komplexním oboru (třetí "modrá" edice) jsem se nějak zasekl na důkazu Mittag-Lefflerovi věty (věta 13.10, strana 302 v českém vydání).
Nemůžu totiž přijít na to, jak věta 13.6 implikuje existenci racionální funkce  , která má všechny póly mimo
, která má všechny póly mimo  (je to hned nad nerovností
(je to hned nad nerovností 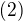 ). Mohl bych samozřejmě použít 13.6 přímo na kompakt
). Mohl bych samozřejmě použít 13.6 přímo na kompakt  , ale pak bych jen věděl, že
, ale pak bych jen věděl, že  má póly mimo
má póly mimo  , což mi nestačí.
, což mi nestačí.
Asi to bude něco triviálního, ale stále se to přede mnou úspěšně skrývá... Děkuji za jakoukoliv radu!
Věta 13.6:
Nechť  je kompaktní množina v
je kompaktní množina v  a
a  je množina bodů obsahující jeden bod z každé komponenty souvislosti množiny
je množina bodů obsahující jeden bod z každé komponenty souvislosti množiny 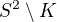 . Pokud
. Pokud 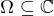 je otevřená,
je otevřená,  ,
, 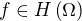 ,
,
a  ,pak existuje racionální funkce
,pak existuje racionální funkce  , jejíž všechny póly leží v předepsané množině
, jejíž všechny póly leží v předepsané množině  , taková, že
, taková, že  pro každé
pro každé  .
.
Důkaz 13.10 v anglickém vydání (české je jen překlad slovo od slova):
Offline
- (téma jako vyřešené označil(a) Mihulik)
#2 26. 04. 2015 08:38 — Editoval OiBobik (26. 04. 2015 09:18)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Problém s důkazem Mittag-Lefflerovy věty
↑ Mihulik:
Ahoj,
pravděpodobně jsem ti totéž odpovídal na MathSE, ale pro jistotu to hodím ještě sem:
Zásadní asi bude informace, že
Každá komponenta
obsahuje komponentu
.
- tedy: každá díra v 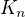 vynikla tak, že "obkrojuje" díru v
vynikla tak, že "obkrojuje" díru v  .
.
Díky tomu je možné body  z věty 13.6 vybrat nejen uvnitř každé komponenty
z věty 13.6 vybrat nejen uvnitř každé komponenty  , ale dokonce tak, aby každý ležel v nějaké komponentě
, ale dokonce tak, aby každý ležel v nějaké komponentě  . Pak budou všechny póly
. Pak budou všechny póly  ležet v
ležet v  , tedy mimo
, tedy mimo  .
.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 26. 04. 2015 10:26
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Problém s důkazem Mittag-Lefflerovy věty (TOTO TÉMA JE VYŘEŠENÉ)