Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » meze kulových (sférických) souřadic - příklad je vyřešený (TOTO TÉMA JE VYŘEŠENÉ)
#2 11. 05. 2015 10:31 — Editoval Rumburak (11. 05. 2015 10:38)
Re: meze kulových (sférických) souřadic - příklad je vyřešený
↑ Nia:
Ahoj.
Mně ten jejich výklad také nepřipadá dvakrát srozumitelný. Důležité je popsat naše těleso  pomocí soustavy nerovnic.
pomocí soustavy nerovnic.
Rozborem rovnic těch ploch a pomocí náčtku zjisíme, že těleso  je průnikem dvou jednodušších množin:
je průnikem dvou jednodušších množin:
- koule určené nerovnicí
(1) 
(ohraničené kulovou plochou o rovnici 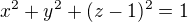 ),
),
- množinou určenou nerovnicí
(2) 
(je to jakýsi rotační kužel o nekonečné "výšce" rozvírající se ve směru osy z, která je zároveň i osou tohoto tělesa).
Na prostředním obrázku je modře vyznačen průmět (do roviny Pxz) nikoliv celého tělesa  , ale pouze jeho poloviny
, ale pouze jeho poloviny
pro  .
.
Meze pro jednorozměrné integrály získané z Fubiniovy věty plynou z nerovnic (1), (2).
Offline
#3 11. 05. 2015 10:39 — Editoval Nia (11. 05. 2015 10:42)
Re: meze kulových (sférických) souřadic - příklad je vyřešený
ahoj/dobrý den,
díky, tak nějak jsem tušila, o jaká tělesa jde. Nepochopila jsem, proč je zobrazen průmět jen poloviny tělesa - měla jsem totiž pocit, že na základě toho jsou určeny ty meze. Já bych třeba 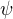 volila od nuly do pí, ale to je evidentně chybně.
volila od nuly do pí, ale to je evidentně chybně.
Ale jak píšete vy, tak stačí ty transformované meze dosadit do rovnic a vypočítat. - Tomu jsem se původně chtěla tak trochu vyhnout a najít jednodušší řešení, ale třeba to jinak nejde: )
Děkuju moc za rady!
Offline
#4 11. 05. 2015 10:51 — Editoval Rumburak (11. 05. 2015 10:55)
Re: meze kulových (sférických) souřadic - příklad je vyřešený
↑ Nia:
To těleso  je symetrické podle roviny
je symetrické podle roviny 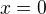 , stačí tedy spočítat objem jeho poloviny pro
, stačí tedy spočítat objem jeho poloviny pro  a tento mezivýsledek
a tento mezivýsledek
vynásobit dvěma.
Těleso  je symetrické i podle roviny
je symetrické i podle roviny  , stačí tedy spočítat objem jeho čtvrtiny pro
, stačí tedy spočítat objem jeho čtvrtiny pro  a tento
a tento
mezivýsledek vynásobit čtyřma.
Z početního hlediska bych se asi přiklonil ke druhé z těchto variant, ale nejde o věc zásadního významu, řekl bych.
Ale bude, myslím, výhodné rozdělit výpočet na kulovou část (sférické souřadnice) a kuželovou část (cylindrické souřadnice).
Offline
#5 11. 05. 2015 11:07 — Editoval Nia (11. 05. 2015 11:21)
Re: meze kulových (sférických) souřadic - příklad je vyřešený
Jasně:) Tak teď už chápu proč je nárysem čtvrtkruh: )
To je pravda - to rozdělení je asi lepší!
Ale kdybych se podívala na to stávající řešení - počítala bych s tím čtvrtkruhem, proč 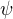 není od nuly do pí? Na základě obrázku níže bych řekla, že by to tak být mělo.
není od nuly do pí? Na základě obrázku níže bych řekla, že by to tak být mělo.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » meze kulových (sférických) souřadic - příklad je vyřešený (TOTO TÉMA JE VYŘEŠENÉ)

