Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 05. 2015 18:54 — Editoval malarad (31. 05. 2015 18:54)
analytická geometrie v rovině
Dobrý den, vypočítal jsem příklad pomocí rovnice kružnice(soustava rovnice přímky a kružnice), ale zajímalo by mě, jestli lze příklad vypočítat i BEZ užití rovnice kružnice.
Zadání:
Na přímce  určete všechny body, které mají od bodu
určete všechny body, které mají od bodu ![kopírovat do textarea $A[1,1]$](/mathtex/75/75f0612cf6a03962dfc68ecef0e30e98.gif) vzdálenost
vzdálenost 
děkuji
Offline
- (téma jako vyřešené označil(a) malarad)
#2 31. 05. 2015 19:10
Re: analytická geometrie v rovině
Ahoj,
tak vzdálenost dvou bodů v rovině je definována jako:
Jeden bod máš ![kopírovat do textarea $A=[a_1;a_2] = [1;1]$](/mathtex/0c/0c4ecc4e52cd7790861733d09e559fce.gif) . Druhý bod, který leží na přímce p, má souřadnice
. Druhý bod, který leží na přímce p, má souřadnice ![kopírovat do textarea $B=[b_1;b_2] = [2y-1;y]$](/mathtex/ad/ad9ea1272bfe0318446880bef6ac0283.gif) .
.
Když dosadíš do výše uvedené rovnice, dostáváš: > vyjdou dvě řešení
> vyjdou dvě řešení
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 31. 05. 2015 19:35 — Editoval misaH (31. 05. 2015 19:37)
#4 31. 05. 2015 19:55
Re: analytická geometrie v rovině
spíš naopak... rovnice kružnice je zakamuflovaný vzorec pro výpočet vzdálenosti dvou bodů v prostoru.
Autor dle mého názoru počítal průsečíky kružnice se středem v [1;1] a poloměrem odmocnina z 5. Toto je trošku něco jiného.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 31. 05. 2015 21:20
Re: analytická geometrie v rovině
↑ malarad:
Můžeš pracovat se směrovým vektorem dané přímky, který má souřadnice (2; 1) a velikost právě  . Jestliže tedy k bodu A přičteš tento vektor a podruhé k bodu A přičteš vektor opačný, dostaneš body na dané přímce příslušně vzdálené.
. Jestliže tedy k bodu A přičteš tento vektor a podruhé k bodu A přičteš vektor opačný, dostaneš body na dané přímce příslušně vzdálené.
Offline
#7 01. 06. 2015 00:29
Re: analytická geometrie v rovině
↑ Al1:
dík, to mě taky napadlo jako první možost, ale až po delší úvaze jsem si uvědomil, že musím do Pythagorovy věty označit odvěsny stejným písmenem, abych neměl jednu rovnici o dvou neznámých(vyjádřit je pomocí poměru směrového vektoru- )
)
Offline
#8 01. 06. 2015 11:53
Re: analytická geometrie v rovině
↑ Freedy:
Ješte prosím Freedyho o vysvětlení, proč 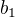 není jen
není jen  ale je
ale je  kde se tam vzala ta mínus jednička? Chápu, že jde o vyjádření x-ové délky pomocí y-ové délky a že x-ová délka je 2 krát větší než ta y-ová, ale ta mínus jednička mi nejde do hlavy...bohužel
kde se tam vzala ta mínus jednička? Chápu, že jde o vyjádření x-ové délky pomocí y-ové délky a že x-ová délka je 2 krát větší než ta y-ová, ale ta mínus jednička mi nejde do hlavy...bohužel![kopírovat do textarea $B=[b_1;b_2] = [2y-1;y]$](/mathtex/ad/ad9ea1272bfe0318446880bef6ac0283.gif)
Offline
#9 01. 06. 2015 11:56
#11 01. 06. 2015 12:17
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: analytická geometrie v rovině
↑ malarad:
No vždyť ten bod B musí ležet na zadané přímce tj. souřadnice bodu musí splňovat zadanou rovnici přímky.
Nikdo není dokonalý
Offline
#12 01. 06. 2015 12:20 — Editoval malarad (01. 06. 2015 12:20)
Re: analytická geometrie v rovině
↑ Cheop:
už mi to taky docvaklo. Teoreticky při mém postupu, kdy bych počítal jen s tím  místo
místo  by přímka s absolutním členem "
by přímka s absolutním členem " " procházela počátekem os souřadnic a sice bych se posunul o správnou vzdálenost jak v x-ové ose, tak v y-ové ose, ale na jiné přímce...Je to tak?
" procházela počátekem os souřadnic a sice bych se posunul o správnou vzdálenost jak v x-ové ose, tak v y-ové ose, ale na jiné přímce...Je to tak?
Offline
#13 01. 06. 2015 12:57 — Editoval Al1 (01. 06. 2015 13:00)
Re: analytická geometrie v rovině
↑ malarad:
V případě  bys hledal body, které mají od A[1; 1]. který na dané přímce neleží, vzdálenost
bys hledal body, které mají od A[1; 1]. který na dané přímce neleží, vzdálenost  . Úplně jiná úloha. V tom případě lze využít řešení pomocí kružnice se středem v A a poloměrem d, nebo řešení nabízeném kolegou Freedym, ale ne jednoduché řešení přes směrový vektor.
. Úplně jiná úloha. V tom případě lze využít řešení pomocí kružnice se středem v A a poloměrem d, nebo řešení nabízeném kolegou Freedym, ale ne jednoduché řešení přes směrový vektor.
Offline
#15 01. 06. 2015 13:32
Re: analytická geometrie v rovině
↑ malarad:
Ahoj.
Pro tentýž bod ![kopírovat do textarea $A[1,1]$](/mathtex/75/75f0612cf6a03962dfc68ecef0e30e98.gif) , ale přímku
, ale přímku  , by se postup navržený kolegou ↑ Al1: musel
, by se postup navržený kolegou ↑ Al1: musel
poněkud upravit:
1) nalézt na přímce  bod
bod  takový, aby přímka
takový, aby přímka 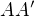 byla kolmá k
byla kolmá k  ,
,
2) hledat na přímce  body mající od
body mající od  vzdálenost
vzdálenost  .
.
(Nakresli si obrázek.)
Offline
