Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 03. 2009 14:21
Stredni a efektivni hodnota
Offline
#2 28. 03. 2009 00:28 — Editoval jelena (28. 03. 2009 00:57)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Stredni a efektivni hodnota
↑ Crovn:
Zdravím :-)
Zkoušela jsem překontrolovat tvoje postupy, ale je to moc nečítelné (myslím, že chyba je, že před integrál vytykáš nějakou čast, což mi nedává příliš smyslu.
Můj postup:
funkce u(t) je lineární:
na intervalu <0, T/3> 
na intervalu <T/3, T> 
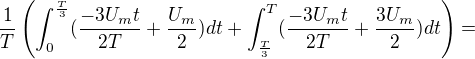


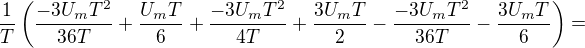
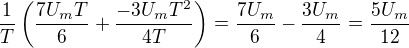
Ještě to překontroluji a snad sepiši i část pro efektivní napětí.
Edit - překontrolováno podle obsahu trojuhelníků a střední hodnota by měla vycházet 5U_m/12 - musím to pohledat (pohledáno - společný jmenovatel :-)
OK?
Offline
#5 28. 03. 2009 13:35 — Editoval jelena (29. 03. 2009 22:37)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Stredni a efektivni hodnota
Tak jsem to začala rozepisovat a uvídím, kam se dostanu (časově, hlavně) - zkusím pokračovat na "efektivní hodnotu":
na intervalu <0, T/3>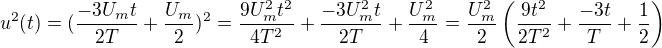
integral funkce na intervalu bude
po dosazeni mezi T/3 a 0 dostaneme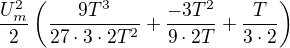
na intervalu <T/3, T>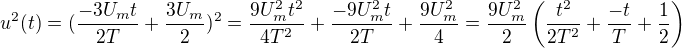
integral funkce na intervalu bude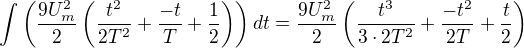
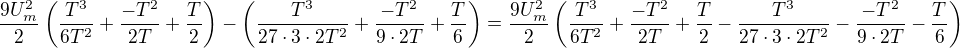
Vysledek - pod odmocninou výsledek integralu - je to potřeba velice pečlivě překontrolovat - sčítání mi dělá velké problémy:
Teď to podělíme T a odmocnime = 
Já na to jestě kouknu, ale nemohu slibovat, že to bude ihned - ale to už jsou úpravy pro ZŠ (které snad nejdou všem, doufám :-), tak to snad překontrolujete a upozornete na chyby.
Offline
#6 28. 03. 2009 13:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Stredni a efektivni hodnota
↑ kotry:
na 1. úseku kolega má funkci klésající, musí být (-) - hledáme předpis lineární funkce y=ax+b a jsou zadány vždy 2 body. OK?
Jinak daleko rychlej by se to va vasich pripadech pocitalo pres obsahy trojuhelníku, obdelníku apod. Ale od vas asi očekavají integrovani - ze ano. Alespon pro kontrolu to pouzijete.
↑ Crovn:
a shodujeme se ve výsledku integrování pro efektivní? - já jsem to dopoledně začala psát s tim, že přerušovaně to snad dopiší, tak to prosím zkontroluj.
Zdravím :-)
Offline
#9 28. 03. 2009 23:30 — Editoval jelena (29. 03. 2009 12:21)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Stredni a efektivni hodnota
↑ kotry:
Zdravím :-)
umět integrovat to opravdu chce :-)
Ale pár poznámek:
dle mého názoru předpis funkce je:
na 1. intervalu (do 1/4 T) je 
na 3. intervalu je 
Nějak se neshodujeme?
Výpočet přes trojuhelníky - integral od u(t) je obsah trojuhelníku pod přímkou u(t). Obsah pravouhleho trojuhelníku je ("odvesná U_m" * odvěsna T/4")/2 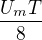 . Jelikož se ten průběh po půlperiodě se opakuje, tak stačí počítat průměrnou hodnotu na první půlperiodě.
. Jelikož se ten průběh po půlperiodě se opakuje, tak stačí počítat průměrnou hodnotu na první půlperiodě.
A otázka moje a možna trochu zavádějící - když máš takový průběh, ve kterém polovina periody hodnota 0 a na druhé polovině pulperody hodnoty jsou přesně opačně k sobě - nemá být průměrná hodnota za celou periodu 0? - editace - tak doufám, že jsem to pochopila správně - pokud se to opačně - symetricky opakuje na pulperiodě, tak se počítá střední hodnota za 1. půlperiodu, jinak by se to opravdu nuloválo.
Děkuji :-)
Offline
#10 29. 03. 2009 14:27
Re: Stredni a efektivni hodnota
Tak jsem to nakonec dopocital podle tech tvych vzorcu a bohuzel to bylo spatne zkousel sem i pro vypocet stredni hodnoty Uo=2/pi*(vysledek Ustred) a Uef=(vysledek efekt)/sqrt(2) a taky spatne, a nakonec kamarad mi po 10minutach rekl ze vysledek je 42 a po dosazenim do vyse uvadenych vzorcu...olala a dobre :D Jeste tedka to nechapu :)
Offline
#13 29. 03. 2009 22:55 — Editoval jelena (29. 03. 2009 22:55)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Stredni a efektivni hodnota
↑ Crovn:
Zdravím :-)
našla jsem jeden překlep při výpočtu efektivní (v první časti pro T/3 uplně na závěr závorky má být 1/2, měla jsem 1/4).
Ale hodnotu 42 nemám - nevím, ani nápad nemám (já bych to stejně počítala přes trojuhelníky, ne přes integraly - tak mi to třeba někdy pozděj dojde, kde je chyba.
Tak doufám, že nejsem nezpůsobila nesplněnou studijní povinnost - to by mi na celé záležitosti vadilo nejvíc.
Ať se daří :-)
Offline
#15 30. 03. 2009 02:01
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Stredni a efektivni hodnota
↑ jelena:Možná poradí Google: http://www.google.cz/search?q=the+answe … everything
(viz též http://www.youtube.com/watch?v=aboZctrHfK8 )
Zkoušel jsem dojít k výsledku i čistě na základě zadaných čísel, ale nikam to nevedlo (resp. vedlo to k výsledku 5/12U_m, který je prý špatně).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#16 30. 03. 2009 17:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Stredni a efektivni hodnota
↑ Kondr:
Ty jsi opravdový poklad :-) Děkuji opravdu velmi moc, ani netušiš, jak jsem něco takového potřebovala v těchto dnech.
Pozděj něco (snad) doplním i k tématu.
Zdravím :-)
Offline




