Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » kompaktnost ve výrokové logice (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 07. 2015 14:11
kompaktnost ve výrokové logice
Ahoj. V knížce pana Švejdara, Logika: neúplnost, složitost a nutnost jsou uvedeny 2 ekvivalentní verze věty o kompaktnosti pro výrokovou logiku:
a) Je-li T množina výrokových formulí taková, že každá její konečná podmnožina je splnitelná, pak T je splnitelná.
b) Máme T množinu výr. formulí a formuli  . Pokud platí
. Pokud platí 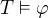 , pak existuje konečná podmnožina
, pak existuje konečná podmnožina 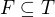 taková, že
taková, že 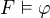 .
.
Je uveden důkaz, že a) implikuje b), je uveden důkaz, že a) platí.
Zajímalo by mě, jestli lze nějak jednoduše dokázat, že i b) implikuje a). Něco jsem zkusila, ale nic z toho nevylezlo.
Díky.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 11. 07. 2015 13:23
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: kompaktnost ve výrokové logice
↑ Andrejka3:
Zdar,
to je tedy v kontextu výrokové logiky?
Pokud jo, tak to jde nějak takto:
Nechť  není splnitelná, buď
není splnitelná, buď  libovolná kontradikce. Pak z definic snadno je vidět, že
libovolná kontradikce. Pak z definic snadno je vidět, že  . Dle (b) je pak
. Dle (b) je pak 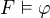 pro nějakou konečnou podmnožinu
pro nějakou konečnou podmnožinu  , tedy vidíme, že
, tedy vidíme, že  je konečná podmnožina
je konečná podmnožina  , která není splnitelná. To je spor.
, která není splnitelná. To je spor.
Pro predikátovou logiku to bude fungovat v podstatě stejně, jen ty symboly znamenají něco trochu jiného.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 11. 07. 2015 19:00
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: kompaktnost ve výrokové logice
↑ OiBobik:
Ahoj, proč není F splnitelná? Plyne to z toho, že spnitelnost se zachovává inkluzí?
(Jinak pokud je důkaz a) snadný, pak je i snadný důkaz implikace b)=>a) :-). Ale předpokládám, že je a) dokazováno pomocí věty o úplnosti a tak zas tak úplně snadná není.)
"Máte úhel beta." "No to nemám."
Offline
#4 11. 07. 2015 19:34
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: kompaktnost ve výrokové logice
↑ check_drummer:
Cau,
F neni splnitelna, jelikoz jeji semanicky dusledek je kontradikce, tj. neco nesplnitelneho.
Jinak dukaz a) se bude dekat skutecne pomoci v. o uplnosti, resp. nejak podobne pomoci axiomu vyberu, pravdepodobne. Tj. Tam je nejaka ta prace.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 11. 07. 2015 22:22
Re: kompaktnost ve výrokové logice
Děkuju za reakce. Týká se to výrokové logiky. Projdu si to.
Jinak, k ačku mám dva důkazy. Jeden přes ordinály a axiom výběru - ten zatím vynechávám. Druhý topologický přes kompaktnost prostoru  . No a pro důkaz kompaktnosti bylo použito tvrzení, že každý filtr je obsažen v nějakém ultrafiltru.
. No a pro důkaz kompaktnosti bylo použito tvrzení, že každý filtr je obsažen v nějakém ultrafiltru.
Na konci je cvičení, kde mám zdůvodnit, proč následující tvrzení jsou v teorii množin bez axiomu výběru ekvivalentní:
1) věta o kompaktnosti výrokové logiky
2) každý filtr je obsažen v nějakém ultrafiltru
3) každý topologický prostor 2^P je kompaktní
Kdybych teda chápala důkaz přes axiom výběru, tak asi mám zadarmo: axiom výběru implikuje 1)
Trochu se v tom motám, ale líbí se mi to.
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 12. 07. 2015 17:32
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: kompaktnost ve výrokové logice
↑ Andrejka3:
Jo no, to je nějak všeobecně známý (ve smyslu: vím to, ale důkaz jsem neviděl : D), že k tomu člověk potřebuje něco trochu méně, než AC, konkrétně většinou se mluví o té 2), tj. o tom tzv Ultrafilter lemma, a skutečně existují modely ZF, kde platí ultrafilter lemma a neplatí AC.
Zajímavé je (pro mě), že je to ekvivalentní větě o kompaktnosti ve výrokové logice, o čemž člověk přemýšlí jako o takové zjednodušené situaci oproti predikátové logice.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#7 12. 07. 2015 17:42 — Editoval Andrejka3 (12. 07. 2015 21:39)
Re: kompaktnost ve výrokové logice
ve smyslu: vím to, ale důkaz jsem neviděl
Tyhle věci se trochu snažím zredukovat -- což možná není dobře. Možná by naopak bylo lepší více věcí vědět a méně umět dokázat.
Aha, takže z ZF + Ultrafilter lemma neplyne ZF + AC.
To cvičení s těmi ekvivalentními tvrzeními se mi i díky nápovědě povedlo dokončit. Teď jdu na syntaktiku. Ale k Ultrafiltrům a AC se vrátím! :D
Zajímavé je (pro mě), že je to ekvivalentní větě o kompaktnosti ve výrokové logice
Jo, zajímavé. A taky ten důkaz je pěkný :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 12. 07. 2015 18:04
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: kompaktnost ve výrokové logice
↑ Andrejka3:
Já to beru tak, že rozumět se snažím věcem, se kterými pracuji nějak často, ale takovýchto kompaktních balíků vět, které člověk typicky jen jako black box aplikuje, mi přijde znát výsledky informativně postačující (vtip je samozřejmě v tom, že člověk nemůže zdaleka nikdy znát všechno do detailu, takže pokud zná všechno do detailů, lze to taky interpretovat tak, že kromě toho, co zná, nezná už nic ani informativně. : D).
Ale to už je úplně off topic.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » kompaktnost ve výrokové logice (TOTO TÉMA JE VYŘEŠENÉ)