Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 07. 2015 13:26 — Editoval jelena (21. 07. 2015 09:40)
- Contemplator

- Příspěvky: 362
- Reputace: 0
Sínusova a kosínusova veta
Dobrý den, mám problém s týmito 2 príkladmy: Vypočítajte dĺžky všetkých strán trojuholníka, ak: (predpoklad- všeobecný trojuholník ABC)
2.
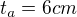
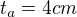

Jelena Edit: úloha (1) je vyčleněna do samostatného tématu. viz pravidla
Offline
#2 20. 07. 2015 13:46
- misaH
- Příspěvky: 13467
Re: Sínusova a kosínusova veta
↑ Contemplator:
Ak sú 2 ťažnice rovnaké, trojuholník je rovnoramenný a 1 ťažnica sa zhoduje s výškou.
Potom už len použiť napríklad Pytagorovu vetu.
Offline
#3 20. 07. 2015 14:51
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Sínusova a kosínusova veta
↑ misaH: prepáč, zle som to napísal, sú rozdielne.
Offline
#4 20. 07. 2015 18:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Sínusova a kosínusova veta
Zdravím,
↑ Contemplator: k úloze 2 kolega Olin předložil takový pěkný návrh (lze využit rovnou nebo pokud máš používat sin/cos věty, také můžeš využit, jelikož v trojúhelnících TT´A a TT´B lze vypočítat všechny prvky pomocných trojúhelníků a pokračovat dál k nalezení všech požadovaných prvků ABC.
Zadání (1) předpokládám, že není problém a dokončíš. Pokud ne, založ si prosím samostatné téma viz pravidla. Děkuji.
Offline
#5 20. 07. 2015 20:00 — Editoval vanok (20. 07. 2015 22:56)
Re: Sínusova a kosínusova veta
pozdravujem,
Poznamka k ulohe 2.
Analyzu daneho problemu mozeme urobit aj pomocou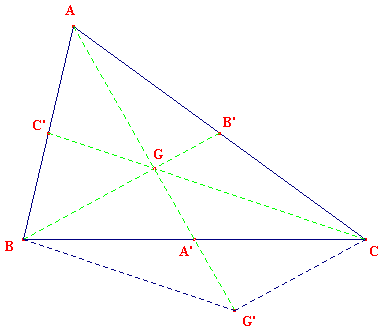
Pochopitelne konstrukcia trojuholnika, ktora z nej vyplyva, musi byt urobena metodou analyza, synteza ... ktoru je potrebne dobre urobit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 21. 07. 2015 07:14 — Editoval jelena (21. 07. 2015 09:39)
Re: Sínusova a kosínusova veta
↑ Contemplator:
Pokud tomu dobře rozumím, máš počítat a ne rýsovat.
Tak tedy nápovědy:
2.Platí:

Vztahy po tb,tc získáš cyklickou záměnou
Označíme-li
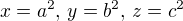 pak dostaneme soustavu 3 lineárních rovnic o 3 neznámých x,y,z
pak dostaneme soustavu 3 lineárních rovnic o 3 neznámých x,y,zOffline
#7 21. 07. 2015 09:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Sínusova a kosínusova veta
Zdravím,
dotaz č. 1 jsem vyčlenila do samostatného tématu pro přehlednost viz pravidla. V tomto tématu navrhuji zůstat u úlohy 2., která již byla různě diskutována
↑ Honzc: v tom smyslu jsem upravila i Tvůj příspěvek. Jinak ani já nepředpokládám, že kolegy bude kreslit, ale počítat. Úloha (spíš náhodou byla tvořena i jen pro ZŠ, ale v závěru byla soustava kvadratických rovnic). Vztah, který navrhuješ, je např. zde u kolegy Kondra s výchozím předpokladem a zde (ale patrně kolega ho bude muset odvodit).
Mělo by ti vyjít
...
Jak jsi hlasoval? :-) Navíc v geometrických úlohách bychom takový zápis neměli používat i pro případné konstrukční záměry za použití kružítka a pravítka. Zdravím (také bratra).
Offline
#8 21. 07. 2015 10:16
Re: Sínusova a kosínusova veta
Ahoj ↑ Honzc:,
Tvoj prispevok je vlastne castou syntezy ( a diskuzie)
Zda sa mi, ze pojem konstrukcia je treba chapat v sirokom zmysle... Tj. vediet ukazat ze vyjadrene vyrazy nam umoznuju, konstruhovat hladany trojuholnik.
Vsak ide o geometricku ulohu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 21. 07. 2015 13:55
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Sínusova a kosínusova veta
Tak k tej 2. by som rád vedel ako z kosínovej vety odvodiť vzťah:  pozeral som aj odkaz od (Kondra) ° , a pomocou prvých 3 riadkov (teda úpravami odvodeného vzťahu) som to skúšal cez maticu.... nejak mi to nevyšlo, ale podstatne je to odvodenie, a ešte, ako sa dostanem k tým ďalším 3 riadkom kde je: a^2, b^2, c^2
pozeral som aj odkaz od (Kondra) ° , a pomocou prvých 3 riadkov (teda úpravami odvodeného vzťahu) som to skúšal cez maticu.... nejak mi to nevyšlo, ale podstatne je to odvodenie, a ešte, ako sa dostanem k tým ďalším 3 riadkom kde je: a^2, b^2, c^2
° 4ta^2=2b^2+2c^2-a^2
4tb^2=2c^2+2a^2-b^2
4tc^2=2a^2+2b^2-c^2
a máme
a^2=(8tc^2+8tb^2-4ta^2)/9
b^2=(8ta^2+8tc^2-4tb^2)/9
c^2=(8tb^2+8ta^2-4tc^2)/9
Offline
#10 21. 07. 2015 15:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Sínusova a kosínusova veta
Zdravím,
↑ Contemplator: odvození samotného vztahu (viz kolega Kondr) souvisí a/nebo se také využívá pro důkaz vlastností rovnoběžníku (součtech čtverců stran a úhlopříček). Kosinová věta bude použita tak, že zapíšeš kos. věty pro trojúhelníky ABD a DCA - viz obrázek, který jsem si vypůjčila odsud s využitím úhlů BDA a ADC. Obdobně pro další těžnice. Měl bys vidět způsob jak eliminovat neznámé úhly BDA a ADC.
Ať se podaří odvodit (případně si můžeš i vyhledat důkaz pro uvedenou vlastnost, ale vlastnoruční odvození se mi zda více prospěšné).
Offline
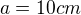

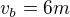 - jediné čo som tu vypočítal je uhol
- jediné čo som tu vypočítal je uhol  a
a 

 a úhlu
a úhlu  Z toho výpočet
Z toho výpočet 
 a úhlu
a úhlu