Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 08. 2015 08:38
Dělení polynomů - proč nevychází?
Ahoj,
snažím se vypočítat příklad :
Výsledek má být:  , ale není, kde mám chybu? Problém nastává někde u druhého kroku dělení...?
, ale není, kde mám chybu? Problém nastává někde u druhého kroku dělení...?
Děkuji za pomoc.
Postup:






Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#3 14. 08. 2015 09:29
Re: Dělení polynomů - proč nevychází?
↑ Al1:
Děkuji za odpověď, zadání jsem kontroloval, je dobře.
Lze tento příklad vložit na wolfram? Nepřišel jsem na to, jak donutit wolfram to vypočítat :-)
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#6 14. 08. 2015 09:55 — Editoval PanTau (14. 08. 2015 10:05)
Re: Dělení polynomů - proč nevychází?
Přikládám příklad od vyučujícího (řešme jen podíl polynomů, zbytek ne)...
ZDE:
Další podíl polynomů co mi nevychází
ZDE (třeba ten  ):
):
Definice dělení je zde, je to jiné dělení než na co jsem zvyklej? Protože i v té definici dělí nějak "divně" ?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#8 14. 08. 2015 10:40
Re: Dělení polynomů - proč nevychází?
↑ Al1:
Děkuji za odpovědi a postupy výpočtů příkladů, ale stále nerozumím tomu, proč vyučující (obrázky jsou přednášky) má jiné výsledky..
Nejde o nějaký zvláštní druh počítání?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#11 14. 08. 2015 16:12
Re: Dělení polynomů - proč nevychází?
Zdravím,
pokud bude zadání:
pak vyjde požadovaný výsledek: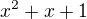
Offline
#12 14. 08. 2015 23:02
Re: Dělení polynomů - proč nevychází?
↑ mák:
Ahoj a děkuji za odpověď,
ale jak se k takovému výsledku dostat?
Bádal jsem nad tím dlouho a "slovně": pokud jsou "v ocásku stejná čísla" tak je "škrtnu" a zbytek jen opíši?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#13 15. 08. 2015 01:02
Re: Dělení polynomů - proč nevychází?
Ahoj,
rovněž můžeš zkusit tento postup



Tedy:
Koeficienty u  jsou rovny 0 u ostatních platí:
jsou rovny 0 u ostatních platí:
1 = a
0 = -a+b
0 = -b+c
0 = a-c
0 = -a+b
0 = -b+c
-1 = -c
Hned je vidět, že a = 1 a c = 1. Zbývá vyjádřit b... 0 = -1 + b >> b = 1
A tedy:
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#15 15. 08. 2015 11:07
Re: Dělení polynomů - proč nevychází?
↑ Brano:
Děkuji za odpověď, pokud tedy tvou odpověď chápu tak při počítání takových příkladů klasicky vydělím polynomy a jelikož je tam pouze 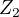 tedy
tedy  tak mě nějaká znaménka nezajímají....
tak mě nějaká znaménka nezajímají....
Protože z tich polynomů tvořím řetězce...
je stejné s
A kdyby bylo například:
je stejné s 
Chápu to tak správně?
Děkuji
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#16 15. 08. 2015 14:28
Re: Dělení polynomů - proč nevychází?
Zdravím,


A teď vykrátit.
Offline
#17 15. 08. 2015 22:07
Re: Dělení polynomů - proč nevychází?
↑ PanTau:
neviem co presne myslis tym "tak me nejaka znamenka nezajimaji"
ale  lebo ich rozdiel (2) je delitelny 2 (napr. mod 3 to neplati) a v polynome mozes (a mal by si) upravit kazdy koeficient tak aby bol iba 0 alebo 1 cize polynom
lebo ich rozdiel (2) je delitelny 2 (napr. mod 3 to neplati) a v polynome mozes (a mal by si) upravit kazdy koeficient tak aby bol iba 0 alebo 1 cize polynom  ma koeficienty
ma koeficienty  co je to iste (mod 2) ako
co je to iste (mod 2) ako  co zodpoveda polynomu
co zodpoveda polynomu 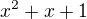
Offline



 se po rozkladu na součin dá zkrátit na tvar
se po rozkladu na součin dá zkrátit na tvar



 cize vysledok mas spravne - a ked si vsimnes tak zvysok je
cize vysledok mas spravne - a ked si vsimnes tak zvysok je  cize to vyslo presne.
cize to vyslo presne.