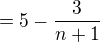Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 10. 2015 17:11
Omezenost posloupnosti
Zdravím, rád bych se tady s vámi poradil o omezenosti posloupností, konkrétně této: 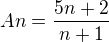 . Nikde jsem nenašel nějaký způsob jak přijít, respektive dokázat, že je posloupnost omezená shora/zdola. Já to dělám tak, že si vypíši prvních několik členů a podle toho poznám, zda-li je pst. omezená nebo není. Konkrétně u této:
. Nikde jsem nenašel nějaký způsob jak přijít, respektive dokázat, že je posloupnost omezená shora/zdola. Já to dělám tak, že si vypíši prvních několik členů a podle toho poznám, zda-li je pst. omezená nebo není. Konkrétně u této: 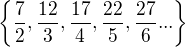 . Z toho vidím, že je omezená zdola těmi
. Z toho vidím, že je omezená zdola těmi  , a shora podle mě není, ale ve výsledcích je napsáno, že je i shora, ale čím ? nekonečno jí přeci nemůže omezit. Lze říci, že pokud má posloupnost sup a inf, tak je omezená ? Pokud jen inf, tak zdola, pokud jen sup. tak shora ?
, a shora podle mě není, ale ve výsledcích je napsáno, že je i shora, ale čím ? nekonečno jí přeci nemůže omezit. Lze říci, že pokud má posloupnost sup a inf, tak je omezená ? Pokud jen inf, tak zdola, pokud jen sup. tak shora ?
Offline
#2 10. 10. 2015 17:28
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Omezenost posloupnosti
Opět zdravím ↑ Hansikii:
Platí, pokud je posloupnost konvergentní je omezené. Obráceně to platit nemusí. Nicméně pokud zjistíš, že je skutečně konvergentní, zjistíš tím i omezenost. Spočítáme tedy limitu této posloupnosti. Je vidět, že je posloupnost rostoucí, tudíž omezenost zdola je asi nejlepší zjistit dosazením prvního členu (n=1), pokud by byla klesající je tato hodnota supremum (byla by horní hranice). Pokud ti vyjde, že je limita rovna v tomto případě  , není shora omezená.
, není shora omezená.
Offline
#3 10. 10. 2015 17:53
Re: Omezenost posloupnosti
Bohužel, limity ještě neovládám, ale pokusím se na to tady přijít sám, popř. s vaší pomocí.u této limity 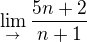 , bych si měl uvědomit, že čitatel tedy
, bych si měl uvědomit, že čitatel tedy jde k
jde k  a jmenovatel taky, takže dostávám tvar
a jmenovatel taky, takže dostávám tvar  , nyní vytknu ten "nejsilnější člen", takže 5n a dostanu tvar:
, nyní vytknu ten "nejsilnější člen", takže 5n a dostanu tvar:  . Další postup už ale nevím
. Další postup už ale nevím
Offline
#4 10. 10. 2015 18:08
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Omezenost posloupnosti
↑ Hansikii:
Jak píšeš máme tuto limitu  , ano obecně platí, že máme tvar
, ano obecně platí, že máme tvar 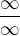 a proto by se dalo použít i L'Hospitalovo pravidlo, kde bychom použili derivace, které jak hádám rovněž neznáš a v tomto případě by nám to pouze přidělalo práci.
a proto by se dalo použít i L'Hospitalovo pravidlo, kde bychom použili derivace, které jak hádám rovněž neznáš a v tomto případě by nám to pouze přidělalo práci.
Je tedy nejlepší vytknout z limity n (vytknout 5n je rovněž správně, ale opět by nám to přidělalo trochu práci).
Dostaneme: 
Nyní je zřejmé, že n/n je 1. Máme tedy  . Toto platí díky pravidlům pro počítání s limitami, dalo by se to přepsat na
. Toto platí díky pravidlům pro počítání s limitami, dalo by se to přepsat na  a platí, že
a platí, že 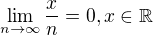
Offline
#5 10. 10. 2015 18:15
Re: Omezenost posloupnosti
↑ xstudentíkx:
Výborně, výborně.. díky vám jsem pochopil princip limitů a postup jak zjistit limity alespoň u těch jednoduchých posloupností, jsem vám za to velmi vděčný, nevěděl jsem jak jinak se vám odvděčit, tak jsem vám, alespoň přidal reputaci :)) Ještě bych se chtěl zeptat, konkrétně u této posloupnosti jsme se dozvěděli, že má limitu 5, dá se z toho odvodit ta omzenost ? popř. jakým vztahem :)
Offline
#6 10. 10. 2015 18:26 — Editoval xstudentíkx (10. 10. 2015 18:31)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Omezenost posloupnosti
↑ Hansikii:
Limity jsou velice zajímavá část matematiky a práce s těmito základními není ani nijak složitá :). Většina lidí si tu automaticky tyká, takže mi spíš tykej :)
Tím, že jsme zjistili limitu posloupnosti, jsme zároveň zjistili určitý bod ke kterému se členy této posloupnosti s rostoucí hodnotou blíží, tím jsme zároveň zjistili její supremum (5), k tomuto číslu se členy blíží a posloupnost je jím tedy omezená. Takže posloupnost je shora omezená číslem 5. Obecně platí, jestliže jsou všechny členy posloupnosti  než nějaké číslo M, je posloupnost shora omezená.
než nějaké číslo M, je posloupnost shora omezená.
Co se týká omezenosti zdola, je zřejmé že to musí být  , jelikož nelze najít menší číslo, kterému by se posloupnost rovnala. Dej si však pozor na rostoucí a klesající posloupnosti :)
, jelikož nelze najít menší číslo, kterému by se posloupnost rovnala. Dej si však pozor na rostoucí a klesající posloupnosti :)
Offline
#7 10. 10. 2015 18:34
Re: Omezenost posloupnosti
↑ xstudentíkx:
Dobře, jestli jsem to tedy pochopil, tak supremum je zároveň limita posloupnosti ? Vypočítáním limity vždycky zjistím jen supremum. Tu obecnou definici uvedenou v poslední větě nevím, jestli jsem dobře pochopil, vlastně se tam tvrdí to co jsem psal na začátku se supremem,že supremum je větší nebo rovno všem číslům posloupnosti a díky tomu je posloupnost shora omezená.
Offline
#8 10. 10. 2015 19:49
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Omezenost posloupnosti
↑ Hansikii:
pokud máme konvergentní rostoucí posloupnost, tak její supremum je skutečně její limita. Nicméně posloupnost může být omezená a přitom nemít limitu. Například 1,-1,1,-1,1,... má supremum 1. Poslední větu jsi pochopil správně :)
Offline
#9 10. 10. 2015 19:58
Re: Omezenost posloupnosti
↑ Hansikii:
Jednoduchy sposob ako spoznat ci je obmedzena tato postupnost: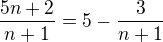
Je jasne, ze zhora je obmedzena, lebo to je 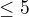 (samozrejme
(samozrejme  su prirodzene). Mozes si vsimnut, ze ked
su prirodzene). Mozes si vsimnut, ze ked  rastie, tak
rastie, tak  klesa a
klesa a 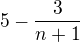 rastie, takze post. je rastuca a zdola obmedzena prvym clenom. Hotovo, bez limit.
rastie, takze post. je rastuca a zdola obmedzena prvym clenom. Hotovo, bez limit.
Offline
#11 10. 10. 2015 21:52 — Editoval Marian (10. 10. 2015 21:53)
Re: Omezenost posloupnosti
↑ Xellos:
Tleskám tvé myšlence, provést vše jednoduše bez limit (to se snad přímo nabízí). Snad bych jen podotknul, že omezenost zdola je možno dokázat (ačkoliv se slabší mezí) také triviálně takto:
Dalo by se to ale vyladit daleko více, ale jedná se mi o co nejvyšší míru triviality řešení původní úlohy.
Offline