Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 10. 2015 21:27
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
je množina těleso?
Pěkný večer,
nejsem si jistá jedné věci týkající se těles.
Mějme množinu ![kopírovat do textarea $\{a+b\sqrt[3]{2}:a,b\in \mathbb{Q}\}$](/mathtex/04/04498c90a5edd3a7c967935d0bd581da.gif) a mám rozhodnout zda se jedná o těleso.
a mám rozhodnout zda se jedná o těleso.
jako první jsem řešila uzavřenost na násobení a z toho mám: ![kopírovat do textarea $(a+b\sqrt[3]{2})(c+d\sqrt[3]{2})=(ac+bd\sqrt[3]{4})+(ad+bc)\sqrt[3]{2}$](/mathtex/11/11c75d577f36683178ea8da830bc1549.gif) lze tedy říci, že pokud
lze tedy říci, že pokud 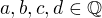 , potom
, potom ![kopírovat do textarea $(ac+bd\sqrt[3]{4}) $](/mathtex/6e/6e265aaa6048ccb31ab8401c414bb8ad.gif) není racionální a
není racionální a 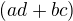 je racionální? Z čehož plyne, že
je racionální? Z čehož plyne, že ![kopírovat do textarea $(a+b\sqrt[3]{2})(c+d\sqrt[3]{2})$](/mathtex/67/6760c7618f2199b170259741f7fb1d35.gif) není racionální a tedy se nejedná o těleso?
není racionální a tedy se nejedná o těleso?
Pokud bych však měla ![kopírovat do textarea $\{a+b\sqrt[]{2}:a,b\in \mathbb{Q}\}$](/mathtex/09/09f3ccd0fae0c20c0d6657e27c292994.gif) potom by uzavřenost na násobení platila.
potom by uzavřenost na násobení platila.
Mám trochu problém s pochopením role toho iracionálního čísla, už jsem to tu na fóru hledala, ale nic z toho mi to neupřesnilo.
Offline
#2 15. 10. 2015 00:20 — Editoval Brano (26. 10. 2015 21:57)
Re: je množina těleso?
spravne sa ti zda, ze to nie je teleso, len to treba poriadnejsie dokazat
najprv, ze preco je tvoj argument "nedostatocny" napr. taka ![kopírovat do textarea $\sqrt[3]{2}+1\cdot\sqrt[3]{2}$](/mathtex/73/73f992f5bf420df5a7d01afcdf1f2ae3.gif) - v druhom clene je ta
- v druhom clene je ta  racionalna a prvy clen nie je racionalny - a predsa to ma spravnu formu, lebo sa to da zapisat ako
racionalna a prvy clen nie je racionalny - a predsa to ma spravnu formu, lebo sa to da zapisat ako ![kopírovat do textarea $0+2\cdot\sqrt[3]{2}$](/mathtex/eb/eb1c082f9520aaca3837d001313bf4b8.gif)
teraz ako dokazat, ze nasobenie nie je uzavrete - tu je lepsie to nerobit vseobecne ale vybrat si napr.![kopírovat do textarea $\sqrt[3]{2}\cdot\sqrt[3]{2}=\sqrt[3]{4}$](/mathtex/9d/9daaaa8ddf7c36d4883b4ec4f8321342.gif) a chceme ukazat, ze sa neda napisat ako
a chceme ukazat, ze sa neda napisat ako ![kopírovat do textarea $a+b\sqrt[3]{2}$](/mathtex/f4/f445705fa8815f1d53055293d568a0a1.gif)
predpokladaj, ze sa da; potom![kopírovat do textarea $\sqrt[3]{4}=a+b\sqrt[3]{2}$](/mathtex/46/4613ffe548204e2180abc9cac6190728.gif) a teda
a teda![kopírovat do textarea $4=a\sqrt[3]{2}+b\sqrt[3]{4}=a\sqrt[3]{2}+b(a+b\sqrt[3]{2})=ab+(a+b^2)\sqrt[3]{2}$](/mathtex/8b/8b696f9faa7b4df578fb2398f9bbbde9.gif)
kedze ![kopírovat do textarea $\sqrt[3]{2}$](/mathtex/e7/e77ed8d8f473e6819793afdd5a121307.gif) je iracionalne, tak potom nutne
je iracionalne, tak potom nutne 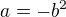 a
a  , cize
, cize 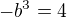 a teda
a teda ![kopírovat do textarea $b=-\sqrt[3]{4}$](/mathtex/c9/c9e818ed0de1762610cbc33529a55e17.gif) co nie je racionalne a to je spor.
co nie je racionalne a to je spor.
EDIT: mam tu chybu - malo to byt ![kopírovat do textarea $2=a\sqrt[3]{2}+b\sqrt[3]{4}=...$](/mathtex/80/80bbb7134ce2bc3a2ac5d2b670933777.gif) co nakoniec da
co nakoniec da ![kopírovat do textarea $b=-\sqrt[3]{2}$](/mathtex/2e/2eaf9bc6b1b2b7ce15a9eb1559a532f4.gif) - cize pointa argumentu ostane ta ista
- cize pointa argumentu ostane ta ista
Offline
#3 15. 10. 2015 10:55 — Editoval vanok (15. 10. 2015 10:56)
Re: je množina těleso?
poznamka
Najmensie teleso, ktore obsahuje rationalne cisla a ![kopírovat do textarea $\sqrt[3]2$](/mathtex/d4/d4ac4e6b4eafc9381d3f75da96dec206.gif) je vytvorene prvkami
je vytvorene prvkami ![kopírovat do textarea $a + b\sqrt [3]2 + c \sqrt[3]4$](/mathtex/fd/fdb1d8810b8297f7931a5cf4ab2a969a.gif) kde a,b,c su rationalne.
kde a,b,c su rationalne.
Tu https://fr.m.wikipedia.org/wiki/Corps_de_rupture najdes po fr zaujimave informacie, ktore ste iste videli v skole.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 15. 10. 2015 15:21 — Editoval xstudentíkx (15. 10. 2015 15:25)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: je množina těleso?
↑ Brano:
Děkuji, tomuto už rozumím a tento důkaz už je skutečně důkazem, na rozdíl od mého.
Ještě takové doplnění, pokud bych chtěla dokazovat inverzní prvek, mám tedy místo dokázání pomocí přímého výpočtu (![kopírovat do textarea $\frac{1}{a+b\sqrt[3]2{}}=\frac{a}{a^{2}-b^{2}\sqrt[3]{4}}-\frac{b}{a^{2}-b^{2}\sqrt[3]{4}}\frac{\sqrt[3]2{}}{1}$](/mathtex/84/840b48b52ffd5a87ae3cab68c6a055a4.gif) ) použít tuto možnost:
) použít tuto možnost: ![kopírovat do textarea $\frac{1}{a+b\sqrt[3]{2}}=\frac{1}{\sqrt[3]{4}}$](/mathtex/96/96f2c5ceb44ad4adb5586d2f1ac62760.gif) nebo-li slovně budu se snažit dokázat, že inverzní prvek se nerovná inverznímu prvku iracionálního čísla, jestliže a nebo b není iracionální.
nebo-li slovně budu se snažit dokázat, že inverzní prvek se nerovná inverznímu prvku iracionálního čísla, jestliže a nebo b není iracionální.
Ještě jak uvádíš, že lepší vybrat si nějaké číslo konkrétně a zvolil jsi ![kopírovat do textarea $\sqrt[3]{4}$](/mathtex/b2/b25a62c927605930bb2d5f7226a5ab16.gif) , jaké další varianty by v tomto případě šly například zvolit?
, jaké další varianty by v tomto případě šly například zvolit?
↑ vanok:
Děkuji za doplnění, škoda, že neumím francouzsky...
Offline
#5 15. 10. 2015 17:05 — Editoval Brano (15. 10. 2015 17:06)
Re: je množina těleso?
uzavrete na inverzne prvky to znova nie je a znova je najlepsie v takom pripade skumat jeden - t.j. konkretne a,b a nie vsetky
napr. ![kopírovat do textarea $\left(\frac{1}{2}\sqrt[3]{2}\right)^{-1}=\sqrt[3]{4}$](/mathtex/58/58c775d0670ff8e574e52ded0cd4cedc.gif) a to uz vieme, ze tam nie je.
a to uz vieme, ze tam nie je.
a k tvojej druhej otazke - aky prvok vyberat. No to musis odhadnut - najlepsie je vybrat taky aby si mala co najjednoduchsi postup. mohla by si skumat aj ![kopírovat do textarea $\sqrt[3]{2}$](/mathtex/e7/e77ed8d8f473e6819793afdd5a121307.gif) a bolo by to trosicku narocnejsie alebo
a bolo by to trosicku narocnejsie alebo ![kopírovat do textarea $1+\sqrt[3]{2}$](/mathtex/fb/fbe50b03bd3b32ef1044fb6b203e59fc.gif) a bolo by to este trochu narocnejsie, ale mohla by si skusit aj napr
a bolo by to este trochu narocnejsie, ale mohla by si skusit aj napr  - a tam neuspejes, lebo "akoze nahodou" inverzny prvok k dvojke je v poli.
- a tam neuspejes, lebo "akoze nahodou" inverzny prvok k dvojke je v poli.
Offline
#6 15. 10. 2015 17:26 — Editoval vanok (15. 10. 2015 17:27)
Re: je množina těleso?
Ahoj ↑ Brano:,
Alebo este jednoduchsie, vyuzi moju poznamku ↑ vanok:
Cize napr. mozes vypocitat ![kopírovat do textarea $(a + b\sqrt [3]2 + c \sqrt[3]4)(a' + b'\sqrt [3]2 + c' \sqrt[3]4)$](/mathtex/12/126010a0fcf91844c864154e393679a3.gif) a predpokladat ze druhy prvok je inverzny prveho a tak ten sucin je 1...atd
a predpokladat ze druhy prvok je inverzny prveho a tak ten sucin je 1...atd
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 15. 10. 2015 18:44
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: je množina těleso?
↑ Brano:
Dobře, tak teď už je mi to jasnější. Budu tedy volit konkrétní hodnoty. Trochu jsem se inspirovala tímto řešením:
(stačí rozkliknout)
Offline
#9 16. 10. 2015 11:20 — Editoval Brano (16. 10. 2015 12:57)
Re: je množina těleso?
Sherlock napsal(a):
↑ Brano:
Zdravím, mám dotaz ohledně uzavřenosti násobení: Kde je psáno, že naše množina musí být podmnožinou racionálních čísel?
a kde to podla teba pozadujem?
Sherlock napsal(a):
↑ Brano:
Nemělo by se spíš dokázat, že?
to som presne dokazoval - tak pripadne sa spytaj presnejsie comu nerozumies
Offline
#10 16. 10. 2015 11:23
Re: je množina těleso?
↑ xstudentíkx:
ved fajn, len tam to vyjde, ze to axiomy pola splna, takze ich dokazujes a teda to treba pre vsetky a,b
ked to vsak nesplna, tak staci najst jeden kontapriklad - nemusis hladat vsetky
Offline
#11 16. 10. 2015 18:42
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: je množina těleso?
↑ Brano:
Jo, tak to skutečně je, už vím jak na to a příklady mi vychází, ještě jednou díky :)
Offline
#12 17. 10. 2015 10:34 — Editoval vanok (17. 10. 2015 23:07)
Re: je množina těleso?
Pozdravujem,
Pre informaciu ![kopírovat do textarea $(a + b\sqrt [3]2 + c \sqrt[3]4)(a' + b'\sqrt [3]2 + c' \sqrt[3]4)=1$](/mathtex/3e/3eb08b1069b0c528b3975fe6eda67e59.gif) da
da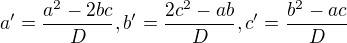 , kde
, kde 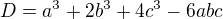 (Kde
(Kde  nie je nula ak aspon jedno z
nie je nula ak aspon jedno z  nie je nula).
nie je nula).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 17. 10. 2015 23:16
Re: je množina těleso?
Technicka poznamka.
Vdaka poznamke ↑ vanok:, ako aj ↑ vanok:, mozte dat odpovede, ktore mozu zovseobecnit polozene otazky v cviceni.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
