Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 10. 2015 18:14
Re: limita gon.funkce
Ahoj,
to je sice pravda, že neexistuje. Tobě ale stačí, že víš, že daná funkce je v nekonečnu omezená.
Pokud je f(x) omezená a  pak
pak 
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 24. 10. 2015 18:47
Re: limita gon.funkce
↑ malarad:
není moc korektní psát 0 do jmenovatele.
Náhodný příklad, co jsi vymyslel řešení mít může.
Například 
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 24. 10. 2015 18:54
Re: limita gon.funkce
↑ Freedy:
já ten náhodný příklad vůbec nemyslel jako limitu, ale jen pro představu jak jsem to zprvu předpokládal. Myslel jsem, že pokud nemá cos limitu v plus nekonečnu, tak celý příklad "nemá řešení"
Psal jsi:
to je sice pravda, že neexistuje. Tobě ale stačí, že víš, že daná funkce je v nekonečnu omezená.
Pokud je f(x) omezená a  pak
pak 
tou funkcí omezenou- f(x) jsi asi myslel to  ??? Omezená je tedy fe funkční hodnotě od -1 do +1, nebo jak vůbec vypadá funkce cos (3x+1) v hodnotě x jde do
??? Omezená je tedy fe funkční hodnotě od -1 do +1, nebo jak vůbec vypadá funkce cos (3x+1) v hodnotě x jde do 
Offline
#6 24. 10. 2015 19:01
Re: limita gon.funkce
↑ malarad:
Zdravím,
platí  , proto řekneme, že je fce omezená. Funkční hodnota, když x jde do
, proto řekneme, že je fce omezená. Funkční hodnota, když x jde do  samozřejmě neexistuje. Fce je periodická s periodou
samozřejmě neexistuje. Fce je periodická s periodou  a její funkční hodnota se mění od -1 do1.
a její funkční hodnota se mění od -1 do1.
Offline
#7 24. 10. 2015 19:03
Re: limita gon.funkce
Ahoj,
je to funkce, která je omezená. To znamená, že limita dané funkce v nekonečnu neodbíhá do +-nekonečna.
Funkce, která nemá limitu v nekonečnu a vůbec by se o ni nedalo bavit by byla například  .
.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#10 24. 10. 2015 19:25
Re: limita gon.funkce
Ještě bych poprosil tedy, jak se mám postavit k tomuto příkladu? Nechci zakládat nový příspěvek, protože to chci přímo porovnat s příkladem úvodním.
tento příklad by měl vyjít jako nekonečno v porovnání s příkladem na začátku tohoto vlákna, proč tedy limita z tohoto příkladu neexistuje?
Offline
#12 24. 10. 2015 20:00
Re: limita gon.funkce
↑ malarad:
Kolega ti napsal jednu z vět o limitě funkce
Pokud je f(x) omezená a  pak
pak 
Ovšem  podmínky věty nesplňuje, tedy tuto větu nelze k výpočtu užít.
podmínky věty nesplňuje, tedy tuto větu nelze k výpočtu užít.
věty o limitách funkcí
Offline
#13 24. 10. 2015 20:00
Re: limita gon.funkce
Ahoj,
funkce cos(x) se pohybuje v intervalu <-1;1>. Jelikož funkce  je rostoucí a má limitu jak si správně napsal
je rostoucí a má limitu jak si správně napsal  tak limita
tak limita  nemůže existovat, jelikož jsi divergentní funkci vynásobil divergentní funkcí.
nemůže existovat, jelikož jsi divergentní funkci vynásobil divergentní funkcí.
Zkrátka daná funkce v nekonečnu osciluje mezi + nekonečnem a - nekonečnem.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline



 =
= 

 je nekonečno, ale funkce samotná stále osciluje ve funkčních hodnotách jako třeba
je nekonečno, ale funkce samotná stále osciluje ve funkčních hodnotách jako třeba 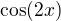 a ve dvojnásobných funkčních hodnotách by to bylo třeba
a ve dvojnásobných funkčních hodnotách by to bylo třeba  , pokud se nemýlím
, pokud se nemýlím =
= 