Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Definice limity posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 11. 2015 10:03
Definice limity posloupnosti
Zdravím,
mám dokázat pomocí definice limity posloupnosti následující:
Napsal jsem si to teda podle definice
Výsledky sice nemám, ale když jsem to zkoušel dopočítat, tak se mi to nějak nezdálo. Poradil by někdo, jak řešit tuto úlohu, kde vystupuje komplexní čísla?
Offline
- (téma jako vyřešené označil(a) Pritt)
#4 17. 11. 2015 11:34
Re: Definice limity posloupnosti
↑ Pritt: Já bych spíš řekl, že to libovolné ale jinak pevně zvolené kladné celé číslo.  neplatí, pokud je "i" imaginární jednotka, protože by ta posloupnost oscilovala. (Uvaž, jak se chová "i" při umocňování.)
neplatí, pokud je "i" imaginární jednotka, protože by ta posloupnost oscilovala. (Uvaž, jak se chová "i" při umocňování.)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 17. 11. 2015 12:25 — Editoval Freedy (17. 11. 2015 12:26)
Re: Definice limity posloupnosti
Ahoj,
limita posloupnosti komplexních čísel je  právě tehdy, když
právě tehdy, když
Z tvé posloupnosti lze vybrat 2 podposloupnosti  , například
, například --->
---> 
 --->
---> 
A máš tedy 2 různé limity vybraných posloupností z posloupnosti an. Tedy původní limita neexistuje.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 17. 11. 2015 13:04 — Editoval Bati (17. 11. 2015 13:34)
Re: Definice limity posloupnosti
↑ Freedy:↑ byk7:
On tam ale má  , což může znamenat komplexní nekonečno, a ne
, což může znamenat komplexní nekonečno, a ne 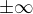 . A potom ta limita je správná, protože
. A potom ta limita je správná, protože  .
.
Speciálně pro ↑ Freedy:: Z té věty, co jsi napsal pouze plyne, že limita neexistuje v  , což je celkem triviální pravda. Ale ta limita existuje v
, což je celkem triviální pravda. Ale ta limita existuje v 
↑ Pritt:
Řešíš tedy nerovnici , kde
, kde  je im. jendotka. Nejdřív upravíš levou stranu:
je im. jendotka. Nejdřív upravíš levou stranu:
Teď by bylo dobrý se nějak zbavit i. Potřebuješ tedy odhadnout shora výraz  , tzn. zespoda výraz
, tzn. zespoda výraz  , aby v něm nebylo i. Jestliže ale
, aby v něm nebylo i. Jestliže ale 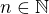 , tak
, tak  , protože vzdálenost mezi 1 a -i je větší než mezi 1 a 0. To samý pro 2, 3, atd. Tzn., že ti stačí najít
, protože vzdálenost mezi 1 a -i je větší než mezi 1 a 0. To samý pro 2, 3, atd. Tzn., že ti stačí najít  , aby pro
, aby pro  platilo
platilo  . Teď už bys to měl dát dohromady.
. Teď už bys to měl dát dohromady.
Offline
#9 17. 11. 2015 14:53
Re: Definice limity posloupnosti
↑ Bati:
to zní logicky. Díky... Takže  je rozšíření komplexních čísel o komplexní nekonečno? Takže limita
je rozšíření komplexních čísel o komplexní nekonečno? Takže limita  v
v  existuje, ale v
existuje, ale v 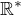 ne, tak?
ne, tak?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#14 17. 11. 2015 21:40
Re: Definice limity posloupnosti
↑ byk7:
správný zápis by ale byl 
stále ale nerozumím tomu, proč je nutné definovat komplexní nekonečno. Vždyť se mohlo zavést takto, ne?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#15 17. 11. 2015 21:45
Re: Definice limity posloupnosti
↑ Freedy:
To nekonečno bez "+" neznamená to samé jako to s "+".
V komplexních číslech se totiž čísla dají porovnávat pouze na základě velikosti, ale ne jako v reálných číslech.
Neplatí a < b, nebo a > b ale |a| <> |b|, čili tam žádné "-" nekonečno ani nemůže být.
Offline
#16 17. 11. 2015 21:48
Re: Definice limity posloupnosti
↑ Pritt: ale to v rozporu není. A chápu, taky že by  bylo něco jiného jako
bylo něco jiného jako  ale chovalo by se to podobně jako komplexní nekonečno.
ale chovalo by se to podobně jako komplexní nekonečno.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#18 17. 11. 2015 22:51
Re: Definice limity posloupnosti
↑ Freedy:
Zápis  se nepoužívá. Tvá definice je hodně divná, jsou tam vlastně jen čtyři body a musíš pracovat s argumenty kompl. čísel. Definice pomocí
se nepoužívá. Tvá definice je hodně divná, jsou tam vlastně jen čtyři body a musíš pracovat s argumenty kompl. čísel. Definice pomocí  je naopak naprosto přirozená, a hodí se např. když chceš rozumně pracovat s funkcemi jako
je naopak naprosto přirozená, a hodí se např. když chceš rozumně pracovat s funkcemi jako  v
v  . Pro podrobnosti si počkej do třeťáku, nebo si přečti tohle, str. 16 - 20.
. Pro podrobnosti si počkej do třeťáku, nebo si přečti tohle, str. 16 - 20.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Definice limity posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)

 .
.
