Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z pravděpodobnosti a statistiky
- » Pomoc s pravděpodobností
#1 23. 11. 2015 19:24
Pomoc s pravděpodobností
Ahoj, při hrabání se jednou sbírkou příkladů jsem narazil na jeden, se kterým opravdu nevím, jak pohnout.
Předmětem příkladu je 100 místné letadlo, které je plně zaplněno. Pasažéři se usazují postupně popořadě. Ovšem první pasažér zapomněl svůj lístek (a tedy i své číslo sedadla, které je jeho), tudíž si sedne na kterékoli náhodné místo. Přichází na řadu další pasažér - pokud někdo sedí na jeho místě, tak mlčí, a sedne si zase na další náhodné místo. Tak to pokračuje až k poslednímu pasažérovi.
Otázka zní, jaká je pravděpodobnost, že poslední pasažér si sedne na to své přidělené místo dle lístku?
Jak říkám, nevím jak s tím pohnout. Snad jen úplně minimální začátek. Pravděpodobnost, že si první pasažér sedne mimo své místo, je 99%, tudíž 1%, že trefí to své.
Zamotal jsem se hlavně v úvaze, která počítá s tím, že pasažér 1 si sedne na náhodné místo a to zrovna bude místo přidělené pasažérovi 2. Pasažér 2 uvidí své místo obsazené a sedne si na náhodné místo a vyjde mu to na místo pasažéra 1. Tím pádem by totiž všichni ostatní pasažéři si posedali, jak mají.
Prosím vás, moudré lidi pravděpodobností oplývající, o osvětlení při postupu, nebo se snad dnes ani nevyspím, jak nad tím stále dumám :-D
Děkuji všem :-)
Offline
#2 24. 11. 2015 10:25
Re: Pomoc s pravděpodobností
Můj nápad je takový: všech možných rozesazení je 100!, všech rozesazení, kde stý pasažér sedí na svém místě je 99!, takže hledaná pravděpodobnost je 99!/100!=1/100.
Ale radši ještě zdůrazním, že kombinatorika není moje silná stránka a může tam být někde chyba v úvaze (já ji ovšem nevidím :).
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#3 24. 11. 2015 15:04
Re: Pomoc s pravděpodobností
Díky za Tvoji odpověď. Takto jednoduché řešení vypadá velmi elegantně, bohužel jsem zatím nesehnal správný výsledek :-(.
Mohl bys jen, prosím, pro mě rozvést, proč se zrovna pravděpodobnost, že poslední stý pasažér si sedne na správné místo, měla rovnat tomuto podílu?
Offline
#4 24. 11. 2015 15:12 — Editoval LukasM (24. 11. 2015 15:29)
Re: Pomoc s pravděpodobností
↑ byk7:
Myslím, že tam chyba je. Ta jednotlivá rozsazení totiž nejsou rovnocenná (v tom smyslu, že by k nim docházelo se stejnou pravděpodobností). Je to jako argumentovat, že pravděpodobnost je 50 % - buď si sedne správně, nebo ne :-) A ironicky je to správná odpověď, byť argumentovat je třeba jinak - ovšem také jsem to bez počítače nevyřešil.
Řešení skrývám a navrhuji přesun do zajímavých úloh.
Řešení hrubou silou (Pascal):
Offline
#5 25. 11. 2015 09:50 — Editoval Honzc (25. 11. 2015 10:38)
Re: Pomoc s pravděpodobností
Offline
#6 25. 11. 2015 14:16
Re: Pomoc s pravděpodobností
Offline
#7 25. 11. 2015 18:10
Re: Pomoc s pravděpodobností
pohleďte a užasněte (nebo mi tam najděte chybu a vysmějte se mi:-))
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z pravděpodobnosti a statistiky
- » Pomoc s pravděpodobností

 pravděpodobnost, že n-tý pasažér obsadí místo tomu poslednímu. Zřejmě
pravděpodobnost, že n-tý pasažér obsadí místo tomu poslednímu. Zřejmě 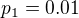 . Pak přijde druhý pasažér, který na svém místě najde buď prvního, nebo volno. Tj.
. Pak přijde druhý pasažér, který na svém místě najde buď prvního, nebo volno. Tj.
 , jak jsem nahoře naznačil. Totéž se druhým pasažérem. Takže
, jak jsem nahoře naznačil. Totéž se druhým pasažérem. Takže
 tedy pravděpodobnost, že n-tý pasažér zasedne místo poslednímu je
tedy pravděpodobnost, že n-tý pasažér zasedne místo poslednímu je
