Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 11. 2015 10:57 — Editoval Ondrik_B (27. 11. 2015 10:58)
Cosinus v limite
Ahoj resim tuto limitu: 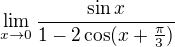
zkousel jsem na cosinus souctovy, ale to nikam nevedlo. Napadlo me pouzit policajty na sin x. Pak by me na jedne strane vychazelo - nekonecno a na druhe + nekonecno. (to ale neznamena ze limita nexistuje, zejo. Protoze kdyz skusim levou a pravou limitu tak vychazeji shodne +nekonecno) . (a/0 je definovany vyraz ze? Rovna se to +/- nekonecno, nebo se mylim?) Tabulkovou limitu cosinu jdouci k nule znam, ale nesla mi tam napasovat.
Prosim o radu.
Dik y.
Offline
- (téma jako vyřešené označil(a) Ondrik_B)
#2 27. 11. 2015 11:48
Re: Cosinus v limite
↑ Ondrik_B:
Ahoj.
Zkusil bych substituovat 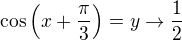 .
.
K tomu bude potřeba ještě vyjádřit 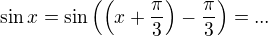 pomocí
pomocí  .
.
Offline
#3 27. 11. 2015 13:00
#4 29. 11. 2015 15:07
Re: Cosinus v limite
↑ Rumburak:
Dekuju, dobra rada. Ted uz si budu pamatovat ze goniometrickou jednici muzu pouzivat pro jakekoliv nasobky x.
Offline

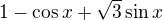 , kde
, kde  .
.