Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 12. 2015 01:48 — Editoval Crashatorr (12. 12. 2015 01:53)
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Konvergence řad
Zdravím, chtěl bych poprosit jestli by mi někdo mohl zkontrolovat důkaz u konvergence řady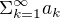 ,
, 
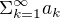 konverguje
konverguje 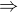
 konverguje
konverguje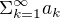 konverguje a tedy existuje
konverguje a tedy existuje kde
kde  pak pro
pak pro  existuje limita
existuje limita  a jestliže
a jestliže  , kde L je kladné.
, kde L je kladné.
Opačná implikace neplatí, protože si vemu třeba  , která konverguje ale
, která konverguje ale  je divergentní. Jen jak by se to dalo dokázat obecně?
je divergentní. Jen jak by se to dalo dokázat obecně?
Předem díky.
Offline
- (téma jako vyřešené označil(a) Crashatorr)
#2 12. 12. 2015 08:28
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Konvergence řad
↑ Crashatorr: Ahoj, to je zbytečné a nemusí to být pravda. Ne jasné, že od jistého k jsou všechna  , tj.
, tj.  , řada je nezáporná a má konvergentní majorantu, tak musí být taky konvergentní.
, řada je nezáporná a má konvergentní majorantu, tak musí být taky konvergentní.
Offline
#3 12. 12. 2015 10:20
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Konvergence řad
↑ OndrasV:
Jo tvůj důkaz chápu a je to o dost jednodušší, ale mohl bys mi prosím napsat proč by to nefungovalo jak jsem psal já? Jinak díky za odpověď.
Offline
#4 12. 12. 2015 10:27
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Konvergence řad
↑ Crashatorr: Neplatí implikace ve směru, že když řada konverguje, musí mít konv. majorantu genometrickou řadu, co třeba  ?
?
Offline
#5 12. 12. 2015 11:01
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Konvergence řad
↑ OndrasV:
Teď asi nechápu co myslíš, mohl bys prosím to napsat podrobněji?
Offline
#6 12. 12. 2015 11:04
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Konvergence řad
↑ Crashatorr: Nemohl, na tom příkladě jsem ukazoval, že když součet řady konverguje, tak to neznamená, že lze použít ten tvůj trik.
Offline
#7 12. 12. 2015 12:02
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Konvergence řad
↑ OndrasV:
Jo takto, dobře děkuji. Jen poslední dotaz, využívá se tedy nutné podmínky konvergence? Pokud ak konverguje pak se její sčítanci blíží k nule a tudíž pro nějaké k už musí platit, že ak<1, tím pádem pak tato řada ohraničuje řadu ak^2, protože ak^2<=ak
Offline
#8 12. 12. 2015 18:08
- OndrasV

- Místo: Praha
- Příspěvky: 513
- Škola: VŠE (1997-2004), FEL (2014-??)
- Pozice: mudrlant
- Reputace: 31
Re: Konvergence řad
↑ Crashatorr: Ano, řekl jste to podle mě zcela přesně.
Offline
#9 12. 12. 2015 18:13
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Konvergence řad
↑ OndrasV:
Ještě jednou díky za pomoc a trpělivost.
Offline