Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 12. 2015 22:26
Kombinatorika - n dětí na kolotoči
Zdravím vás!
Mám úlohu, se kterou si dost dlouho už lámu hlavu, ale moje pokusy o zdolání byly všechny neúspěšné. Prosím o pomoc.
Na kolotoči sedí  dětí (
dětí ( ), počáteční rozmístění je na obrázku. Určete, kolika způsoby lze děti rozmístit tak, aby nové rozmístění neobsahovalo tyto uspořádané dvojice:
), počáteční rozmístění je na obrázku. Určete, kolika způsoby lze děti rozmístit tak, aby nové rozmístění neobsahovalo tyto uspořádané dvojice: 
V počátečním stadiu kolotoč (při prvním rozesazení) vypadá popořadě jako posloupnost čísel (dětí) od jedničky do  , na
, na  pak navazuje do cyklu jednička. Přečetl jsem si jeden postup, kde se ten počet rozesazení počítá jako množina vzniklá průnikem všech možných rozesazení, kde v jednom rozesazení není
pak navazuje do cyklu jednička. Přečetl jsem si jeden postup, kde se ten počet rozesazení počítá jako množina vzniklá průnikem všech možných rozesazení, kde v jednom rozesazení není 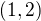 , v dalším není
, v dalším není  atd.
atd.
Řešení vypadá takto: 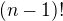 (což je počet všech rozesazení jakožto permutací dětí)....tedy:
(což je počet všech rozesazení jakožto permutací dětí)....tedy:
Vidím v tom inkluzi exkluzi, ale nevidím přesně, co se počítá. Hlavně se nevyznám v těch kombinačních číslech. Prosím nakopněte mě. Dík.
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#2 17. 12. 2015 00:14
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Re: Kombinatorika - n dětí na kolotoči
↑ Makrofág:
Ahoj, když je to PIE, neměla by se spíš uvažovat ta rozesazení, která naopak (1,2) obsahují? (A podobně další.)
"Máte úhel beta." "No to nemám."
Offline
#3 17. 12. 2015 00:17
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Re: Kombinatorika - n dětí na kolotoči
Jinak komb. číslo  se t tex píše {n \choose k}. Škoda, že tak důležitý symbol není v nápovědě symbolů vpravo.
se t tex píše {n \choose k}. Škoda, že tak důležitý symbol není v nápovědě symbolů vpravo.
"Máte úhel beta." "No to nemám."
Offline
#4 17. 12. 2015 01:11
Re: Kombinatorika - n dětí na kolotoči
↑ check_drummer:
Ano, máš pravdu. Přepsal jsem se. Počítá se to jako průnik množin, kde tam ty uspořádané dvojice jsou. Co znamenají ta kombinační čísla v řešení?
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#5 18. 12. 2015 16:49
- check_drummer

- Příspěvky: 5168
- Reputace: 106
Re: Kombinatorika - n dětí na kolotoči
↑ Makrofág:
Podle mě by to měl být počet způsobů, kterým lze zvolit konkrétní dvojice - např. je-li těchto dvojic k, tak je tam podle toho  . Jenomže podle mého je problém v tom, že některé dvojice mohou mít společné prvky a tak si nejsem jist, zda je ten vzoreček správně...
. Jenomže podle mého je problém v tom, že některé dvojice mohou mít společné prvky a tak si nejsem jist, zda je ten vzoreček správně...
"Máte úhel beta." "No to nemám."
Offline
