Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 09. 2014 22:46 — Editoval lucyyye (17. 09. 2014 22:47)
Nevlastní limita posloupnosti
Dobrý den, potýkám se zrovna s dvěma příklady. Celý princip posloupností i limit asi chápu. Jenom nevím, jak bych měla dokázat tyto příklady.
Dokažte, že aritmetická posloupnost (a )∞n=1, a1= -2, d = 1, má nevlastní limitu +∞.
)∞n=1, a1= -2, d = 1, má nevlastní limitu +∞.
Dokažte, že posloupnost (-2 )∞, má nevlastní limitu -∞.
)∞, má nevlastní limitu -∞.
Děkuji předem za rady.
Offline
#2 18. 09. 2014 10:57 — Editoval Rumburak (19. 09. 2014 10:16)
Re: Nevlastní limita posloupnosti
Ahoj.
Zkus to dokázat z definice nevlastní limity.
V prvním případě uvažuj (abstraktní) reélné číslo  a hledej číslo
a hledej číslo  (obecně závislé na
(obecně závislé na  )
)
takové, aby pro všechny indexy  splňující
splňující  platilo
platilo  . Pomůže vzorec pro n-tý člen.
. Pomůže vzorec pro n-tý člen.
Pokud se podaří takové číslo 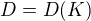 nalézt, ať již zvolené číslo
nalézt, ať již zvolené číslo  by bylo jakkoliv velké,
by bylo jakkoliv velké,
bude tím požadovaný důkaz hotov.
Obdobně u té geometrické posloupnosti.
Offline
#4 18. 12. 2015 15:16
Re: Nevlastní limita posloupnosti
↑ Rozárka96:
Ano, i takto by bylo možno vést příslušný důkaz, za předpokladu, že máme již k disposici vhodnou větu ,
například (stručně a schematicky zapsáno):
Jestliže 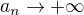 a
a  je omezená, potm
je omezená, potm 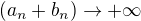 .
.
Mnou navržený důkaz pracuje pouze s definicí limity.
Offline


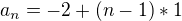
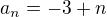
 , kde n se blíží do nekonečna
, kde n se blíží do nekonečna