Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lingebra komutujici matice (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 12. 2015 18:33
Lingebra komutujici matice
Ahoj prosim o radu s timto prikladem:
Popiste vsechny matice X, ktere komutuji s matici:
V podstate tedy resim maticovou rovnici: 
Jedno reseni je mi jasne. X=
Ale nevim jak urcit dalsi reseni, popripade jak urcit kolik reseni existuje. Predem Dik y.
Offline
- (téma jako vyřešené označil(a) Ondrik_B)
#2 23. 12. 2015 19:50
Re: Lingebra komutujici matice
Ahoj ↑ Ondrik_B:
Niekolko poznamok
Ak sa limitujes na matice (2,2)
Potom aj  , kde k je lubovolne cislo m, vyhovuje
, kde k je lubovolne cislo m, vyhovuje
A najdes este nieco ine?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 25. 12. 2015 22:32
Re: Lingebra komutujici matice
↑ Ondrik_B:,
Je ich o mnoho is u viac
To co som uz napisal ti da matricove polynomy
Na uplne riesenie pouzit vlastne hodnoty matice.....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 25. 12. 2015 22:53
Re: Lingebra komutujici matice
↑ vanok:
Celkovym resenim tedy je to co jsme napsaly vyse +  kde
kde 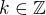 Nebo to jeste neni vsechno?
Nebo to jeste neni vsechno?
Dukaz ze tento polynom resi nasi rovnici udelam tak, ze dle pravidla distributivity roznasobim levou i pravou stranu rovnice a zjistim ze se rovnaji.
Diky.
Offline
#6 25. 12. 2015 23:43
Re: Lingebra komutujici matice
pozri aj
Commuting matrices na google.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 26. 12. 2015 09:18
Re: Lingebra komutujici matice
Este jedna metoda
Poloz
Dosad to do danej maticovej rovnice a vyries potom najdeny lin. system.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 26. 12. 2015 13:51
Re: Lingebra komutujici matice
↑ vanok:
To je asi nejlepsi zpusob. Nasel jsem vyjadreni pro y a z v zavisloti na dvou parametrech x a t. Soudim ze toto je celkove reseni, ktere zahranuje vsechny priklady ktere jsme zminili vyse.
Offline
#9 26. 12. 2015 21:55
Re: Lingebra komutujici matice
↑ Ondrik_B:
Ano. A je to pekne aktivita kde sa toho mozes vela naucit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lingebra komutujici matice (TOTO TÉMA JE VYŘEŠENÉ)

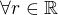
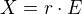 kde E je jednotkova matice 2x2.
kde E je jednotkova matice 2x2.