Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Minima a maxima funkce jedné proměnné (klikový mechanismus)
#1 29. 12. 2015 11:36 — Editoval FliegenderZirkus (29. 12. 2015 18:35)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Minima a maxima funkce jedné proměnné (klikový mechanismus)
Obrázek:
Poloha pístu u klikového mechanismu na obrázku je daná funkcí
 ,
,kde všechny parametry kromě
 jsou konstanty. Dále při konstantní úhlové rychlosti
jsou konstanty. Dále při konstantní úhlové rychlosti  platí
platí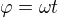 a derivováním (1) dostaneme rychlost pístu
a derivováním (1) dostaneme rychlost pístu![kopírovat do textarea $v(\varphi) = \omega \cdot \left[ -r\sin \varphi - \frac{r\cos\varphi \cdot \left(r\sin\varphi - e\right)}{\sqrt{l^2-\left(r\sin\varphi-e\right)^2}} \right] \quad (2)$](/mathtex/2a/2a9e047271b1ef8fd1dcc9f34bd9e414.gif) ,
,obdobně zrychlení je
![kopírovat do textarea $a(\varphi) = \omega ^2\cdot \left[-r\cos \varphi + \frac{r\sin\varphi \cdot \left(r\sin\varphi - e\right)-r^2\cos^2\varphi}{\sqrt{l^2-\left(r\sin\varphi-e\right)^2}} - \frac{r^2\cos^2\varphi \left(r\sin\varphi-e\right)^2}{\left(l^2-\left(r\sin\varphi-e\right)^2\right)^{3/2}}\right] \quad (3)$](/mathtex/30/3098a90992360c49a903a0bfbf69aa76.gif) .
.K dotazu: snažím se najít minima a maxima funkcí (1) až (3). Pro (1) to není příliš velký problém, stačí vyřešit (2)=0 což lze na papíře. Pro extrémy rychlosti a zrychlení už to ale na papíře jde dost těžko a nejsem si ani, jistý jestli nějaké analytické řešení existuje. Proto jsem chtěl zkusit použít CAS, ale WolframAlpha ani Maxima se nikam nedostaly. Rád bych se proto zeptal, jestli někdo máte tip jak formulovat vstup pro WA nebo nějaký jiný program aby to zvládnul popř. zda rovnou vidíte, že pokoušet se o analytické řešení nemá smysl. Předem díky za reakce!
Offline
#2 29. 12. 2015 14:51
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Minima a maxima funkce jedné proměnné (klikový mechanismus)
↑ FliegenderZirkus:
Ahoj, asi zderivovat ručně, upravit na zlomek a dát WA hledat nulový bod čitatele.
"Máte úhel beta." "No to nemám."
Offline
#3 29. 12. 2015 19:06
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Minima a maxima funkce jedné proměnné (klikový mechanismus)
↑ check_drummer:
Ahoj, zkusil jsem tu rovnici a=0 upravit a trochu zjednodušit na![kopírovat do textarea $-\cos\varphi \cdot (l^2-(r\sin\varphi-e)^2)^{3/2}+[\sin\varphi\cdot (r\sin\varphi-e)-r\cos^2\varphi]\cdot (l^2-(r\sin\varphi-e)^2)-r\cos^2\varphi \cdot (r\sin\varphi-e)^2=0$](/mathtex/83/83943f87c5e31725cb894e18a54eb40a.gif) ,
,
ale ani takto WA nic nevyplivne.
Teprve když zvolím číselné hodnoty parametrů, WA spočítá řešení numericky. Tím myslím můžu své snahy s čistým svědomím vzdát?
Offline
#4 30. 12. 2015 14:25
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Minima a maxima funkce jedné proměnné (klikový mechanismus)
↑ FliegenderZirkus:
Aha, ty tam máš parametry - tak to je asi skoro bez šance získat nějaký "explicitní vztah", resp. musela by to být velká náhoda (a mít nástoj umožňující symbolické výpočty). Ještě bych zkusil substituci "tan(x/2)", pomocí které lze získat rovnici jen v té proměnné. Ale pak asi získáš rovnici, kterou stejně nebude možné řešeit explicitně.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Minima a maxima funkce jedné proměnné (klikový mechanismus)
