Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 12. 2015 15:39 — Editoval marcel1423 (30. 12. 2015 15:45)
- marcel1423
- Příspěvky: 38
- Reputace: 0
Inverzní zobrazení
Mám příklad:
Mějme funkci  danou předpisem
danou předpisem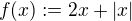
Nalezněte vzor množiny  . Nalezněte inverzní funkci
. Nalezněte inverzní funkci  , existuje-li.
, existuje-li.
Výsledek:
Snadno nahlédneme
Pro inverzní funkci platí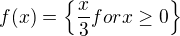

Hledaným vzorem je 
Zajímá mě jak se přijde že hledaný vzor  jde mi o tu -1.
jde mi o tu -1.
Plus jestli mi někdo může poradit jak náhledneme do abych věděl co je menší než 0 a co má být větší než nula (viz. složené závorky výše).
Budu rád za jakékoliv rady.
Offline
#2 30. 12. 2015 16:05
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Inverzní zobrazení
Zdar.
Jednak kulturu psaní v TeXu lze zlepšit nahlédnutím např. do tohoto materiálu
http://www.penguin.cz/~kocer/texty/lsho … t2e-cz.pdf
na stránku 46 a dál, aby člověk nemusel špičatou závorku psát většítkem/menšítkem, nebo čipku mínusem a většítkem :-).
Jak se přijde na to, co je v těch složených závorkách?
Jednak to nemá být ve složených závorkách, protože nejde o množiny. A jednak tam má být vždy  , ne
, ne  .
.
Přijde se na to tak, že se zinvertuje zadaný předpis. Nejdřív se musí dosadit za absolutní hodnotu, tím se předpis rozrůzní pro záporná a nezáporná x a na každé reálné poloose se pak invertuje zvlášť. Invertovat jde taky graficky - nakresli si graf zadaného f a zobraz ho souměrně podle osy prvního a třetího kvadrantu.
Na vzor zadané množiny se přijde jejím zadáním jako vstupu do inverzní funkce.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#3 30. 12. 2015 16:21
Re: Inverzní zobrazení
↑ marcel1423:
Ahoj .
Funkce f je rostoucí a spojita, nulu zobrazuje na nulu. Funkce k ní inversní má tytéž vlastnosti.
Našel jsi ji dobře, ale špatně označil.
Pro  je tedy
je tedy  , jinde
, jinde 
Interval  si rozdělíme na části
si rozdělíme na části  a vzor budeme hledat ke každé zvlášť.
a vzor budeme hledat ke každé zvlášť.
Offline