Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 01. 2016 16:37
Ještě jedna limita
Dobrý večer,
tak mám ještě jeden problém, který je nejspíš úplně triviální, ale já to v tom prostě nevidím.
Zkouším nějak upravit
ale pořád se jen točím v kolečku a sebemenší úprava vede vždy na podobnej tvar.
Hrubou silou jsem se vrátil až na začátek příkladu, což také nebylo moc k užitku.
Díky moc.
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 02. 01. 2016 22:38
Re: Ještě jedna limita
Pozdravujem.
Alebo zase Taylor okolo 0.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 03. 01. 2016 01:41
Re: Ještě jedna limita
↑ Pavel:
ano, k tomuto jsem samozřejmě také došel, nicméně L'hospital je ..... asi nemusím zmiňovat..
↑ vanok:
když není L'hospital, tak logicky neni ani Taylor. Sice by to s ním bylo lehčí, ale bohužel.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 03. 01. 2016 02:05 — Editoval vanok (03. 01. 2016 13:01)
Re: Ještě jedna limita
Staci Taylor okolo 0
1/2+x/12+O(x^2).
Edit. Oprava
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 03. 01. 2016 11:00
Re: Ještě jedna limita
↑ Freedy:
Dobrý den.
Nevím, zda jde o korektní a v daném problému rozumně využitelnou úvahu:
Pokud dodefinujeme hodnotu funkce  v bodě x = 0 její limitou
v bodě x = 0 její limitou  ,
,
pak bych řekl, že
Pokud se tedy nemýlím.
Offline
#8 03. 01. 2016 11:13
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Ještě jedna limita
↑ Jj:
Já jsem si nad touto limitou a zejména nad limitou z nedávna lámal hlavu dost dlouho. Na tadytu věc s derivací jsem přišel taky, ale když jsem si pak f v tom odkazovaném případě zderivaval, vyšla obludnost, do které stejně nešla nula dosadit, a tak by to vedlo na nějakou tu větu o výpočtu derivace limitou derivací zleva/zprava, ovšem to se pak má limitit ta obludnost, což se mi dělat nechtělo. Říkal jsem si, že to snad musí jít udělat ještě nějak jinak, bez nových obludností. :-)
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#9 03. 01. 2016 11:37
Re: Ještě jedna limita
↑ Sergejevicz:
Jojo :), obludnosti jako by se tam nějak 'indukovaly'.
Pokud se tedy nemýlím.
Offline
#11 03. 01. 2016 12:29
Re: Ještě jedna limita
↑ Freedy:
Tak tedy bez l'Hospitala:
Využijeme identitu
Ukážeme, že platí silnější tvrzení, tj. existuje limita oboustranná.
Označíme
Položíme substituci 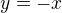 . Pak
. Pak
Obě limity sečteme:
Tj.  , a tedy původní limita vychází
, a tedy původní limita vychází
Jednostranná limita zprava vychází samozřejmě stejně.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#12 03. 01. 2016 13:27
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Ještě jedna limita
jarrro napsal(a):
...v okolí kladnej nuly...
Podivný výraz "kladná nula" a její sestra "záporná nula". Správně se říká pravé resp. levé okolí nuly. Nula je nula, nula je jen jedna. V knihách jsem zatím pojem kladná/záporná nula rozumě zavedený neviděl. A i kdyby byl, tak uvažujme, že je to pravé/levé okolí nuly, ne? Co by pak ale bylo jeho okolí? Okolí pravého/levého okolí nuly? To je divné, ne?
Jinak tenhle postup s označením limity L a odvozením rovnice pro L jsem tu na fóru už někdy viděl. Připomíná mi to per partes pro integrál ze sin*cos.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#13 03. 01. 2016 13:55
Re: Ještě jedna limita
↑ Pavel:
Krásné řešení. Děkuji. :// takovýto postup mě při řešení limit vůbec nenapadne.
jinak díky
↑ Jj: ↑ Sergejevicz: ↑ jarrro: za vaše nápady ;)
F
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#14 03. 01. 2016 14:35
Offline

