Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 07. 01. 2016 19:37 — Editoval jelena (08. 01. 2016 10:56)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Povrchy těles
↑↑ kolop:
děkuji, popisuješ dobře, ale úlohu nejde řešit jen nakreslením a poměřením rozměrů, co máš na obrázku. Obrázek použiješ jen jako pomůcku. Povrch koule je 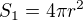 , povrch kuželu máš dobře, ale označíme
, povrch kuželu máš dobře, ale označíme  - poloměr podstavy, aby se to nepletlo s
- poloměr podstavy, aby se to nepletlo s  - poloměrem koule
- poloměrem koule  . Najít poměr, to znamená najít vztah mezi povrchy při podělení, tedy poměr
. Najít poměr, to znamená najít vztah mezi povrchy při podělení, tedy poměr  .
.
K úloze se vrátím k návodu z ↑↑ příspěvku 6:. Trojúhelník  je takový univerzální pro tento výpočet (je pravoúhlý a má stejný úhel u vrcholu
je takový univerzální pro tento výpočet (je pravoúhlý a má stejný úhel u vrcholu  , jako další trojúhelníky, co jsme v řezu nakreslili - my budeme pro výpočty potřebovat
, jako další trojúhelníky, co jsme v řezu nakreslili - my budeme pro výpočty potřebovat  ). Pro další výpočet můžeš využívat podobnost nebo goniometrické funkce, ale měl bys začít od ujasnění rozměrů trojúhelníku
). Pro další výpočet můžeš využívat podobnost nebo goniometrické funkce, ale měl bys začít od ujasnění rozměrů trojúhelníku  . Projdi ještě jednou, prosím, předchozí příspěvky, kde je podrobnější popis.
. Projdi ještě jednou, prosím, předchozí příspěvky, kde je podrobnější popis.
Obrázek - zde je naznačen  , doplň, prosím jeho rozměry a udělej si jasno ohledně podobnosti s trojúhelníkem
, doplň, prosím jeho rozměry a udělej si jasno ohledně podobnosti s trojúhelníkem  - která strana je podobna s kterou a co z toho pro úlohu budeme mít. Pokračuj, prosím.
- která strana je podobna s kterou a co z toho pro úlohu budeme mít. Pokračuj, prosím.
EDIT: doplněno odvození vztahů:
z trojúhelníku  : strany
: strany  ,
,  , z Pythagorovy věty
, z Pythagorovy věty 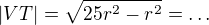
z trojúhelníku  :
: 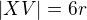 (zároveň je to výška kuželu), potřebujeme stranu
(zároveň je to výška kuželu), potřebujeme stranu  (poloměr podstavy kuželu) a stranu
(poloměr podstavy kuželu) a stranu 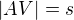 (boční stěna kuželu).
(boční stěna kuželu).
Z podobnosti uvedených trojúhelníků platí: 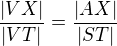 , z toho vztahu bude vyjádření pro
, z toho vztahu bude vyjádření pro  (poloměr podstavy), obdobný vztah použit také pro vyjádření
(poloměr podstavy), obdobný vztah použit také pro vyjádření 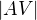 .
.
Offline
#28 07. 01. 2016 20:36 — Editoval misaH (07. 01. 2016 20:42)
- misaH
- Příspěvky: 13459
Re: Povrchy těles
↑ kolop:
A čo z môjho postupu nechápeš?
Žiadnu podobnosť netreba, naozaj.
1. Zapíšeš obsah pravouhlé ho trojuholníka dvoma spôsobmi, z čoho dostaneš  , kde s je prepona toho trojuholníka a R je polomer podstavy kužeľa.
, kde s je prepona toho trojuholníka a R je polomer podstavy kužeľa.
2. Zapíšeš Pytagorovu vetu pre ten pravouhlý trojuholník s využitím odvodené ho vzťahu z bodu 1. Priamo dostaneš, že 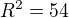
3. Napíšeš požadovaný pomer povrchov - priamo vyjdú 4/9, teda 4:9.
Offline
#36 08. 01. 2016 11:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Povrchy těles
Zdravím,
↑ kolop: je zbytečné se takto hodnotit - spíš bych řekla, že tato úloha je pro Tebe těžká. Jelikož nemáš napočítáno z předchozích látek a postupně. A paní učitelka by to měla vědět - nejspíš to i odvodí, že porovná li Tvou první odevzdanou práci a nový kompletní postup, usoudí, že to není výsledek samostatné práce. Pro klasifikaci "4" bys v této úloze nemusel dojit úplně ke konečnému výsledku, ale mít obrázek s vyznačením všeho, co jde, mít zapsány vzorce pro povrchy a co je poměr povrchů, vyznačit rozměry, co potřebuješ pro výpočty.
Lepší, než na fórech, se domluvit s některou spolužačkou, které to jde, nebo někde v okolí zjistit, zda někdo ze studentů nevyučuje ne moc za dráho. A s paní učitelkou se domluvit, že místo tohoto jednoho složitějšího vypočítáš a doneseš více méně náročných základních výpočtů, ale bude zřejmé, že jsi počítal sám a dokážeš to i předvest před paní učitelkou nebo před třídou.
Do příštího týdne jsem mimo PC, do příspěvku ↑ č. 26: jsem ještě doplnila část odvození rozměrů, ale raději bych věděla, že záležitost s úlohou budeš s paní učitelkou řešit jinak, bez podvádění.
Offline


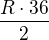 .
. alebo nerozumieš?
alebo nerozumieš?