Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 11. 01. 2016 23:50
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Integrál
Tak ten první integrál, na to je přímo vzorec, a ten druhý je jako přichystaný na substituci - v čitateli čeká něčí derivace :-).
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#8 12. 01. 2016 00:20
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Integrál
↑ malarad:
Je.
Jak píše ↑ Bati:, je dobrý nápad představit si x jako dvojnásobný argument a přepsat podle toho všechny cosiny a siny. Ukáže se pak snadno možnost substituce tg(x/2), nebo jiný trik.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#9 12. 01. 2016 00:21 — Editoval Bati (12. 01. 2016 00:24)
Re: Integrál
↑ malarad:
Je to dobře, musí se to shodovat. Nejspíš přehlížíš nějakou úpravu.
Předpokládám, že ti vyšlo  , ale v učebnici je
, ale v učebnici je  , ne?
, ne?
Offline
#10 12. 01. 2016 00:24
Re: Integrál
↑ Sergejevicz:
díky,
z prvního integrálu vyjde 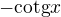 ten je tabulkový, z toho druhého jsem spočítal
ten je tabulkový, z toho druhého jsem spočítal
jak tyto dva výsledky dají výsledek, co je v učebnici- ?
?
Offline
#12 12. 01. 2016 00:30
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Integrál
Rozepiš si cotg pomocí cos a sin, uprav na společného jmenovatele (C nech stranou) a pak se podívej na x jako na dvojnásobek argumentu, tj. x = 2*(x/2) a použij vzorce pro sin a cos dvojnádobného argumentu. Tím se ti tam dostanou ty poloviny x, pak ještě v čitateli použiješ goniometrickou jedničku, něco se zkrátí a zbyde ti ten cotg(x/2).
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#14 12. 01. 2016 00:35
Re: Integrál
Stejně ale doporučuju použít tu fintu, co jsem doporučoval na začátku. Jde o to, že rozšíření  funguje jen pro
funguje jen pro  , což se ve finále projeví jako zbytečně omezující požadavek, protože výsledek
, což se ve finále projeví jako zbytečně omezující požadavek, protože výsledek  je definován i v těchto bodech, narozdíl od toho tvého výsledku.
je definován i v těchto bodech, narozdíl od toho tvého výsledku.
Offline
#16 12. 01. 2016 23:50
Re: Integrál
↑ malarad:
Zdravím.
Drobná substituce (můžete ji třeba dělat jen "v hlavě"): 
a dostanete tabulkový integrál:
Pokud se tedy nemýlím.
Offline



 =
= 
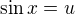


 =
=  =
=  =
=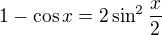 , lze výseldek napsat rovnou.
, lze výseldek napsat rovnou.
 =
=
 .
. .
.