Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 01. 2016 22:18
Provaz
:) Něco pro lidi ze základní školy.
Máme pomeranč. Ten kolem průměru omotáme provázkem.
Provázkem také omotáme celou zeměkouli (v tomto případě koule) kolem průměru.
Nyní oba provázky prodloužíme o 1 metr a tím pádem vznikne mezera mezi pomerančem a provázkem (provázek bude stále kružnice se středem ve středu pomeranče/zeměkoule)
Otázka je, jaký bude rozdíl mezi mezerou mezi pomerančem a provázkem a zeměkoulí a provázkem.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#2 14. 01. 2016 22:33
Re: Provaz
↑ Freedy:
Pro zakladni skolu bych otazku formuloval trochu jinak.
Napriklad bych se zeptal, jestli pod provazkem proleze mys.
Je to daleko nazornejsi na predstavu..
(Existuje jeste podobna, ale ta uz je obtiznosti pro vejsku; kdyz se provaz zvedne pouze na jednom miste, proleze zirafa? )
Offline
#4 16. 01. 2016 18:50
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Provaz
Pavel napsal(a):
↑ lucash:
Kdyby jenom žirafa, i Petřínská rozhledna se pod provaz bez problému vejde.
Ahoj, jak to? Resp. pochopil jsem zadání úlohy, že prodloužíme provaz o 1m a zvedneme jej na jednom místě?
"Máte úhel beta." "No to nemám."
Offline
#5 16. 01. 2016 18:55
Re: Provaz
↑ check_drummer:
Ano, taky jsem se divil, ale vychází mi to opravdu tak. Chystám ukázat své řešení.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 16. 01. 2016 22:01
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Provaz
↑ Pavel:
Aha, asi budeme musel zvolit tečnu k povrchu Země.. ale i tak je to překvapivé. na druhou stranu, ona je země křivá "dovnitř" (vzhledem k té tečně) a ta křivost se tedy musí kompenzovat dostatečnou vzdáleností od Země.
"Máte úhel beta." "No to nemám."
Offline
#7 16. 01. 2016 23:58 — Editoval Pavel (17. 01. 2016 00:05)
Re: Provaz
Modelujme Zemi jako kružnici  se středem
se středem  ve středu Země a poloměrem
ve středu Země a poloměrem  . Zvedneme-li provaz pouze na jednom místě, pak po jeho napnutí vznikne lomená čára, jejíž obě části jsou tečnami ke kružnici, viz obrázek níže.
. Zvedneme-li provaz pouze na jednom místě, pak po jeho napnutí vznikne lomená čára, jejíž obě části jsou tečnami ke kružnici, viz obrázek níže.
Úkolem je zjistit délku úsečky  .
.
Trojúhelníky 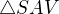 a
a 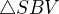 jsou shodné a navíc pravoúhlé. Proto platí
jsou shodné a navíc pravoúhlé. Proto platí![kopírovat do textarea $
|AV|=|BV|&=r\tan\left(\frac{\alpha}2\right)\\[.5\baselineskip]
|SV|&=\frac{r}{\cos\left(\frac{\alpha}2\right)}
$](/mathtex/87/879670b8962abeba391d37e6039ac882.gif)
Proto 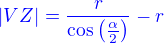 .
.
Délka  prodlouženého lana o 1m je dána vztahem
prodlouženého lana o 1m je dána vztahem 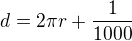 . Na druhé straně lze tuto délku určit jako součet délky konvexního oblouku
. Na druhé straně lze tuto délku určit jako součet délky konvexního oblouku  (tj. toho delšího), délky úsečky
(tj. toho delšího), délky úsečky 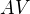 a délky úsečky
a délky úsečky  , tj.
, tj.
Dostáváme rovnici s neznámou  :
:
Bohužel rovnice je analyticky neřešitelná. Prostřednictvím programu Mathematica v 10.3.1.0 jsem určil její přibližné řešení:
Dosazením do modrého vztahu tak získáme přiblížnou výšku napnutého provazu v bodě uchopení nad zemským povrchem, tj.
PS. Místa, kde se provaz začne od země zvedat, tj. vzdálenost bodů A a B, jsou od sebe vzdálena ca o 78,737 km
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 17. 01. 2016 08:56 — Editoval Honzc (19. 01. 2016 06:08)
Re: Provaz
↑ Freedy:
Kdysi jsem řešil podobnou úlohu jako ↑ Pavel: pouze trochu modifikovanou.
Na zeměkouli položme trubku o průměru 3m. (bylo to voleno tak,aby jí prošel slon)
Otázka: o kolik musíme prodloužit obvod zeměkoule, aby provaz obepínal zeměkouli a položenou trubku?
Mám někde řešení, ale teď ho nemohu najít (snad ho zítra najdu-dnes se mi řešit znovu nechce), ale pokud mne paměť neklame pak řešením bylo něco kolem 3-4mm.
Jinak původní úloha je zcela triviální:
původní obvod: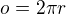
nový obvod (s prodloužením): 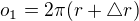 a také
a také  kde
kde  je prodloužení
je prodloužení
Pak 
Protože (jak vidno)  nezávisí na poloměru kružnice, je mezera u všech kružnic stejná, závislá pouze na prodloužení
nezávisí na poloměru kružnice, je mezera u všech kružnic stejná, závislá pouze na prodloužení 
Pzn.: Na tuto úlohu jsem kdysi na vojně (cca před 35-ti lety) vyhrál litr vína (podotýkám, že na pokoji byli všichni spolubydlící vysokoškoláci a nikdo z nich mi nevěřil, že to tak je. Dokonce jsme dělali pokus s provázkem, kdy r=0 a pak s uhlákem)
Po editaci: Řešení slon.
Offline

