Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 01. 2016 21:26 — Editoval fyzika (19. 01. 2016 21:51)
krivkovy integral
zdravim,
mam problem s nasledujucim prikladom -
Pre ktoré realne hodnoty  krivkový integrál
krivkový integrál 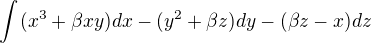 nezávisí od cesty v
nezávisí od cesty v 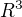 ?
?
__________________________________________________________________________
Riesil som to v zmysle teorie a teda  cize
cize 
Zo zadania 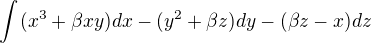 som si oznacil jednotlive zlozky
som si oznacil jednotlive zlozky
ako  ,
,  ,
, 
_____________________________________________________________________________
A čo z toho vyslo?  Cize z toho mi vyplyva, ze aj ked zvoolim realnu hodnotu
Cize z toho mi vyplyva, ze aj ked zvoolim realnu hodnotu  ,tak mi ostane
,tak mi ostane  ... Teda neexistuje realne
... Teda neexistuje realne  ?
?
Robim niekde chybu? Dakujem
Offline
- (téma jako vyřešené označil(a) fyzika)
#2 19. 01. 2016 23:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: krivkovy integral
Zdravím,
složky mám sice jinak uspořádány (pohodlnější je jen porovnávat složky po dvojicích, tak jsou hned rovnice do soustavy, pokud by byla k řešení), ale ve výsledku se shoduji - také mi vychází, že není  . Úloha je z nějaké sbírky, je možné náhled? Děkuji.
. Úloha je z nějaké sbírky, je možné náhled? Děkuji.
Offline
#3 20. 01. 2016 07:27
Re: krivkovy integral
↑ jelena:úloha pravdepodobne nie je z mnou známej zbierky, našiel som ju medzi príkladmi z minulých rokov, ktore sa vyskytovali na skuskach. Pozeral som to viackrat, ale zadanie je skutocne taketo, ziadny preklep...
Cize podla vsetkeho skutocne neexistuje riesenie.
Offline
#5 20. 01. 2016 12:07
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: krivkovy integral
↑ fyzika:
Mně se nelíbí toto:
Asi jsi myslel , ne?
, ne?
A hlavně, já to znám tak, že pro vektorové pole  platí
platí , tedy SYMBOLICKY jde pomocí vektorového součinu psát výsledek operátoru
, tedy SYMBOLICKY jde pomocí vektorového součinu psát výsledek operátoru  použitého na vektor
použitého na vektor  takto:
takto: ,
,
kde  je operátorový vektor, a totiž
je operátorový vektor, a totiž  .
.
Píšu "symbolicky", protože operace  značí vektorový součin, ale ten by znamenal násobitení jednotlivých složek násobených vektorů mezi sebou, ale tady nejde o násobení složek, ale o aplikaci parciální derivace na složku, což násobení není, ale při vypuštění toho operátoru na vektor se to jako násobení chová. Značení s vektorovým násobením vektorů chápu jako mnemotechnickou pomůcku.
značí vektorový součin, ale ten by znamenal násobitení jednotlivých složek násobených vektorů mezi sebou, ale tady nejde o násobení složek, ale o aplikaci parciální derivace na složku, což násobení není, ale při vypuštění toho operátoru na vektor se to jako násobení chová. Značení s vektorovým násobením vektorů chápu jako mnemotechnickou pomůcku.
To symbolické značení je fyzikální a není zcela doslovné a přesné, jak vidíme. Já bych proto v tomto případě byl za to značit například  místo
místo  , aby bylo odlišeno to, že nejde o násobení složek ale o aplikaci parc. derivací.
, aby bylo odlišeno to, že nejde o násobení složek ale o aplikaci parc. derivací.
Myslím tedy, že výsledek by mohl být jinak.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#6 20. 01. 2016 12:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: krivkovy integral
↑ Sergejevicz:
Zdravím,
s kolegou jsme teoretický předpoklad rozebírali v předchozím tématu (a také se mi nelibí uspořádání složek u kolegy - viz můj první příspěvek - používám pomůcku, že na příslušnou souřadnicovou pozici patří rozdíl zbývajících "pozic" parciálně zderivovaných do kříže). Pro snadnou záměnu jednodušší je porovnat složky do rovnic (za předpokladu parciální derivace podle správné proměnné).
Myslím tedy, že výsledek by mohl být jinak.
zkontroluj to, prosím. Děkuji.
Offline
#7 20. 01. 2016 12:26 — Editoval fyzika (20. 01. 2016 12:37)
Re: krivkovy integral
↑ Sergejevicz:ak tomu spravne rozumiem, tak by som zderivoval  ,
,  ,
,  , podla
, podla 
V tom pripade by bolo 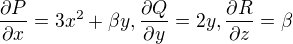 ??? Len potom ako to aplikujem na
??? Len potom ako to aplikujem na  ???
???
Offline
#8 20. 01. 2016 12:30 — Editoval fyzika (20. 01. 2016 12:31)
Re: krivkovy integral
↑ Sergejevicz:
↑ jelena: takze toto usporiadanie jednotlivych zloziek je v poriadku ? :)
takze toto usporiadanie jednotlivych zloziek je v poriadku ? :)
Offline
#9 20. 01. 2016 16:17 — Editoval Sergejevicz (20. 01. 2016 16:20)
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: krivkovy integral
fyzika napsal(a):
↑ Sergejevicz:ak tomu spravne rozumiem, tak by som zderivoval
,
,
, podla
Chceš P, Q a R derivovat podle  , což je vektor a ještě navíc operátorový? To je nesmysl, ne? :-).
, což je vektor a ještě navíc operátorový? To je nesmysl, ne? :-).
fyzika napsal(a):
V tom pripade by bolo
,...
Asi jsi myslel derivovat P podle x, Q podle y a R podle z, viď?
fyzika napsal(a):
Len potom ako to aplikujem na
???
No jak je vidět z vzorce pro  , tak to do něj aplikovat nejde, protože se tam zrovna tyhle parciální derivace nevyskytují. Zato se tam vyskytuje parc. derivace P podle y, P podle z, Q podle x atd. Vždyť se do toho vzorce podívej. Musíš si napočítat ty parc. der., které v něm jsou, a pak je do něj dosadit a porovnat každou složku s nulou (potenciální vektorové pole musí mít nulovou rotaci).
, tak to do něj aplikovat nejde, protože se tam zrovna tyhle parciální derivace nevyskytují. Zato se tam vyskytuje parc. derivace P podle y, P podle z, Q podle x atd. Vždyť se do toho vzorce podívej. Musíš si napočítat ty parc. der., které v něm jsou, a pak je do něj dosadit a porovnat každou složku s nulou (potenciální vektorové pole musí mít nulovou rotaci).
A ano, tento vzorec pro  je správně. Lze ověřit, když se hledá ve skriptech a knihách, nebo na netu.
je správně. Lze ověřit, když se hledá ve skriptech a knihách, nebo na netu.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#10 20. 01. 2016 19:54
Re: krivkovy integral
↑ Sergejevicz: Tak potom má tvoj príspevok zmietol... veď tie špeciálne destinácie som spočítali a uviedol ešte v úvodnom príspevku a kopírovali aj do tohoto príspevku. Akurát že by sa zmenilo poradie jednotlivých zložiek,no rotacia nebude nulová a teda ide mi o to, ci tá úloha má vôbec riešenie.
Tak potom má tvoj príspevok zmietol... veď tie špeciálne destinácie som spočítali a uviedol ešte v úvodnom príspevku a kopírovali aj do tohoto príspevku. Akurát že by sa zmenilo poradie jednotlivých zložiek,no rotacia nebude nulová a teda ide mi o to, ci tá úloha má vôbec riešenie.
Offline
#12 20. 01. 2016 21:22
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: krivkovy integral
fyzika napsal(a):
Akurát že by sa zmenilo poradie jednotlivých zložiek,no rotacia nebude nulová a teda ide mi o to, ci tá úloha má vôbec riešenie.
Pořadí složek obecně je důležité. A i kdyby teď zrovna v tomto případě nebylo, tak je dobré používat správné vzorce :-). Jestli v tom nemáš někde chybu, tak ta úloha řešení nemá.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#13 20. 01. 2016 21:32
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: krivkovy integral
↑ fyzika:
A ještě si zkontroluj znamínka u prvních dvou složek, jak tak na to koukám, tak já je mám opačná. Dělají to ty mínusy před druhou a třetí složkou.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#14 20. 01. 2016 21:59
Re: krivkovy integral
↑ Sergejevicz:zámienka sú opačne kvôli rozdielu jednotlivých zložiek, samozrejme, boli kladne, no po odpočítaní sú už záporne. Ja tam teda chybu nevidím: )
Offline
#15 20. 01. 2016 23:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: krivkovy integral
Zdravím,
↑ fyzika: možné nedorozumění se znaménky se ujasní, pokud minusy v zadání pošleš do závorek: a až potom použiješ P, Q, R.
a až potom použiješ P, Q, R.
Jestli v tom nemáš někde chybu, tak ta úloha řešení nemá.
tedy shoda, děkuji.
Offline
