Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 22. 01. 2016 10:08
Re: Limita
↑ malarad:
Dobrý den.
Pokud L'Hospital, tak bych to zkusil spíš "naopak":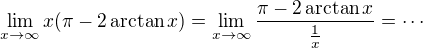
Řekl bych, že to bude jednodušší.
Pokud se tedy nemýlím.
Offline
#4 22. 01. 2016 10:16 — Editoval Sergejevicz (22. 01. 2016 10:41)
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: Limita
↑ malarad:
Je ![kopírovat do textarea $\lim_{x\to\infty}x\(\pi - 2 \arctan x\) =
[\text{subst. }y=\arctan x]
\lim_{y\to\frac{\pi}{2}-} \tan y\(\pi - 2y\) =\\
=\lim_{y\to\frac{\pi}{2}-} \frac{\sin y}{\cos y}\(\pi - 2y\) =\\
= \lim_{y\to\frac{\pi}{2}-} \sin y\cdot\frac{\pi - 2y}{\cos y} =\dots$](/mathtex/01/01b87c3c5aa1320bffdf418a3a24396b.gif)
Roděl na součin limit, v druhé použij 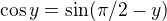 a substituci za lineární dvojčlen, vyjde tam standardní limita. Výsledek je smysluplný výraz, takže rozdělení na součin limit je odůvodněno.
a substituci za lineární dvojčlen, vyjde tam standardní limita. Výsledek je smysluplný výraz, takže rozdělení na součin limit je odůvodněno.
EDIT: Myslím, že u většiny limit je skoro jasné, že LH není povolen a má se to zkusit upočítat elementárně. :-)
EDIT 2. Opraveno x na y po substituci.
EDIT 3: Substituce je odůvodněna např. prostotou fce arctan.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline