Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 01. 2016 23:02 — Editoval Optix (24. 01. 2016 23:29)
Konvexní funkce
Ahoj všem, budu strašně vděčný za jakoukoli pomoc. Dostal jsem se k úloze kde mam ověřit zda funkce je konvexní zadání je že mame matici A typu n x m a víme ze existuje nezáporné řešení y, 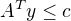 a chtěl bych zjistit zdali je funkce
a chtěl bych zjistit zdali je funkce .
.
Moc nevim jak postupovat, chtěl jsem to ověřovat přímo z definice jako přes  ale to jsem dospěl jen k tomu, že ta množina bez minima je konvexní, tak nevim jestli mužu prohlásit ze pak i to min je konvexní (z důvodu ze funkce je konvexní kdyz epigraf je konvexní a tady je to tak nejak podobne).
ale to jsem dospěl jen k tomu, že ta množina bez minima je konvexní, tak nevim jestli mužu prohlásit ze pak i to min je konvexní (z důvodu ze funkce je konvexní kdyz epigraf je konvexní a tady je to tak nejak podobne).
Předem vsem moc dekuju za pomoc
Offline
- (téma jako vyřešené označil(a) Optix)
#3 25. 01. 2016 09:48 — Editoval Optix (25. 01. 2016 09:49)
Re: Konvexní funkce
Díky Brano,
ale mohl bys mi prosím ještě nějak poradit jak s tím definičním oborem?
asi tam musím využít tu informaci že existuje to nezáporné řešení 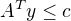 .
.
Ještě bych měl jednu otázku, když do tohoto zadání zkusím vložit konkrétní hodnoty, třeba v jednorozměrném případě a vložím 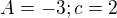 pak nezáporné y existuje např. 0, ale daná funkce mi vychází jako
pak nezáporné y existuje např. 0, ale daná funkce mi vychází jako![kopírovat do textarea $f(b) = 0, b\in (-\infty ,0]$](/mathtex/dd/dd0fc61ff9c4a733c30f885523752246.gif) a
a  a taková to funkce není konvexní na R
a taková to funkce není konvexní na R
Offline
#4 25. 01. 2016 22:20 — Editoval Brano (25. 01. 2016 23:04)
Re: Konvexní funkce
no to sa tam podla mna nehovori, ze ma byt konvexna na R ale snad iba na svojom definicnom obore ktory v tvojom pripade je ![kopírovat do textarea $(-\infty,0]$](/mathtex/8a/8a0c60e734275374cde9b17a902fd0f6.gif) ; ale v podstate ak chces pripustat aj nekonecne hodnoty ako legalne hodnoty f-ka tak tvoj priklad je funkcia ktora je konvexna na R preco by nemala byt?
; ale v podstate ak chces pripustat aj nekonecne hodnoty ako legalne hodnoty f-ka tak tvoj priklad je funkcia ktora je konvexna na R preco by nemala byt?
no a prvej otazke moc nerozumiem ... asi, ze ako sa dokaze ta ohranicenost zdola - tak to je pomerne trivialne
Offline

 je na danej mnozine zdola ohranicene
je na danej mnozine zdola ohranicene su take
su take  , ze existuje nezaporne riesenie
, ze existuje nezaporne riesenie  )
)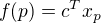 a
a 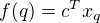 kde
kde  a teda aj
a teda aj 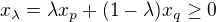 . A kedze
. A kedze 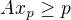 a
a 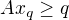 tak potom
tak potom . Teda
. Teda