Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 30. 01. 2016 20:19
Re: funkcionalna rovnica
Zřejmě jste ěkde dělil nulou, protože  je taky řešením, které je spojité v 1.
je taky řešením, které je spojité v 1.
Ještě se mi řešení nepodařilo dotáhnout do konce, ale zatím jsem došel k tomu, že hledaná funkce musí být sudá, 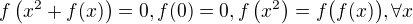 . Nevím ale, jestli to k něčemu bude.
. Nevím ale, jestli to k něčemu bude.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#3 30. 01. 2016 21:15
Offline
#4 31. 01. 2016 00:26 — Editoval Brano (31. 01. 2016 00:27)
Re: funkcionalna rovnica
Offline
#5 31. 01. 2016 03:20
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: funkcionalna rovnica
↑ BakyX:
Ahoj, f(1) lze volit libovolně? Pokud ne, tak jak (a proč)?
"Máte úhel beta." "No to nemám."
Online
#6 31. 01. 2016 08:29
Re: funkcionalna rovnica
1^6 - 2^6 + 3^6 = 666
Offline
#7 31. 01. 2016 14:12
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: funkcionalna rovnica
↑ BakyX:
Podle mě je tedy potřeba to dotáhnout, např. takto:
"Máte úhel beta." "No to nemám."
Online

 take, ze pre vsetky realne
take, ze pre vsetky realne 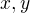 plati
plati 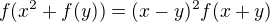 .
. je spojita v
je spojita v  mi vyslo jedine riesenie
mi vyslo jedine riesenie 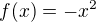 . Ale vseobecny pripad neviem.
. Ale vseobecny pripad neviem. , z čoho
, z čoho 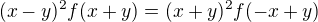 a teraz položiť
a teraz položiť 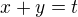 ,
, 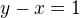 , kde
, kde  je ľubovoľné reálne číslo.
je ľubovoľné reálne číslo.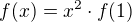 . Dosadením do rovnice potom dopočítame možné hodnoty
. Dosadením do rovnice potom dopočítame možné hodnoty 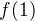 ...
...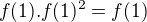 , tj. po úpravě f(1).(f(1)-1).(f(1)+1). Takže v úvahu připadají jen tvary f =0, =-x^2, =x^2, z nichž ten poslední dle mého nevyhovuje a ty první dva ano - což jsou jediná řešení.
, tj. po úpravě f(1).(f(1)-1).(f(1)+1). Takže v úvahu připadají jen tvary f =0, =-x^2, =x^2, z nichž ten poslední dle mého nevyhovuje a ty první dva ano - což jsou jediná řešení.