Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 25. 02. 2016 09:43
Re: Řada 1
↑ Tomas5:
Ahoj. S tou nápovědou už jo..:
Akorát by mě zajímalo, z čeho plyne nápověda.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 25. 02. 2016 09:56 — Editoval Honzc (25. 02. 2016 10:01)
Re: Řada 1
↑ Tomas5:
Nápovědou jsi podle mne moc nepomohl, protože to by se muselo také dokázat.
Vím, že to není důkaz, ale podívej se na obrázek.
Offline
#5 25. 02. 2016 10:07
Re: Řada 1
↑ Tomas5:
Bez nápovědy:
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 25. 02. 2016 16:48 — Editoval Anonymystik (25. 02. 2016 16:55)
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Řada 1
↑ Tomas5: Kolika způsoby mohu vystoupat schodiště, pokud při jednom kroku se posunu nahoru buď o jeden schod, nebo o dva schody? Označme počet těchto způsobů 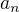 Počet těchto způsobů vyjádřím dvěma způsoby:
Počet těchto způsobů vyjádřím dvěma způsoby:
1) Rozdělím si všechny způsoby na dvě disjunktní podmnožiny. Buď posledním krokem mé cesty bude posun o jeden schod, nebo posun o dva schody. Pokud poslední krok mé cesty byl posun o jeden schod, pak jsem předtím měl  možností, jak se dostat na jeden schod před koncem. Pokud poslední krok mé cesty byl posun o dva schody, pak jsem předtím měl
možností, jak se dostat na jeden schod před koncem. Pokud poslední krok mé cesty byl posun o dva schody, pak jsem předtím měl 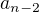 možností, jak se dostat na druhý schod před koncem. Celkový počet způsobů, jak cestu provést, je
možností, jak se dostat na druhý schod před koncem. Celkový počet způsobů, jak cestu provést, je 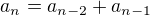 . Je zjevné, že
. Je zjevné, že  . Rekurentní závislost a počáteční podmínka ukazuje, že posloupnost
. Rekurentní závislost a počáteční podmínka ukazuje, že posloupnost  je vlastně posunutá Fibbonacciho posloupnost - tedy
je vlastně posunutá Fibbonacciho posloupnost - tedy  . Proto
. Proto  .
.
2) Uvažme tentokrát, že schodiště má délku 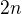 . Cestu přes schodiště si rozdělím opět na disjunktní podmnožiny, podle toho, kolik jsem na cestě udělal kroků po dvou schodech. Předpokládejme, že jsem jich udělal právě
. Cestu přes schodiště si rozdělím opět na disjunktní podmnožiny, podle toho, kolik jsem na cestě udělal kroků po dvou schodech. Předpokládejme, že jsem jich udělal právě  . Pak zbylý počet schodů je
. Pak zbylý počet schodů je 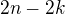 , které jsem přešel kroky, kde jsem se posunoval jen o jeden schod. Udělal jsem tedy celkem
, které jsem přešel kroky, kde jsem se posunoval jen o jeden schod. Udělal jsem tedy celkem 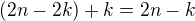 kroků, z čehož jich
kroků, z čehož jich  bylo po dvou schodech, zbytek po jednom schodě. To šlo provést právě
bylo po dvou schodech, zbytek po jednom schodě. To šlo provést právě  způsoby. Nyní musíme posčítat všechny disjunktní podmnožiny, tj. sčítat před všechna vhodná
způsoby. Nyní musíme posčítat všechny disjunktní podmnožiny, tj. sčítat před všechna vhodná  . Přitom zjevně
. Přitom zjevně 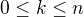 . Celkový počet je tedy
. Celkový počet je tedy 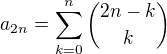 .
.
Srovnáním 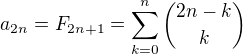 . Nahrazením
. Nahrazením  jsem dokázal, že platí nápověda.
jsem dokázal, že platí nápověda.
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline

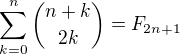 .
.
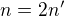 :
: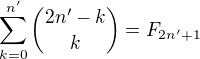 . Položme
. Položme  -- v sumě taky probíhá od nuly do
-- v sumě taky probíhá od nuly do 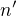 .
. . Levou stranu stačí upravit vztahem
. Levou stranu stačí upravit vztahem a dostaneme dokazované.
a dostaneme dokazované.

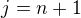 , tj.
, tj.  .
.
![kopírovat do textarea $
F_{2n+3}&=F_{2n+1}+F_{2n+1}+F_{2n-1}+F_{2n+3}+\dots+F_3+F_1
=F_{2n+1}+\sum_{m=0}^{n}F_{2m+1}\\[.5\baselineskip]
&=\sum_{k=0}^n{n+k\choose 2k}+\sum_{m=0}^{n}\sum_{k=0}^m{m+k\choose 2k}
=\sum_{k=0}^n{n+k\choose 2k}+\sum_{k=0}^n\sum_{m=k}^{n}{m+k\choose 2k}\\[.5\baselineskip]
&=\sum_{k=0}^n{n+k\choose 2k}+\sum_{k=0}^n\sum_{m=k}^{n}\left[{m+k+1\choose 2k+1}-{m+k\choose 2k+1}\right]\\[.5\baselineskip]
&=\sum_{k=0}^n{n+k\choose 2k}+\sum_{k=0}^n\biggl[{n+k+1\choose 2k+1}-\underbrace{{2k\choose 2k+1}}_{=0}\biggr]\\[.5\baselineskip]
&=\sum_{k=0}^n{n+k\choose 2k}+\sum_{k=0}^n{n+k+1\choose 2k+1}
=2+\sum_{k=1}^n{n+k\choose 2k}+\sum_{k=0}^{n-1}{n+k+1\choose 2k+1}\\[.5\baselineskip]
&=2+\sum_{k=0}^{n-1}{n+k+1\choose 2k+2}+\sum_{k=0}^{n-1}{n+k+1\choose 2k+1}
=2+\sum_{k=0}^{n-1}{n+k+2\choose 2k+2}\\[.5\baselineskip]
&=2+\sum_{k=1}^{n}{n+k+1\choose 2k}
={\color{blue}\sum_{k=0}^{n+1}{n+k+1\choose 2k}}
$](/mathtex/f1/f10c3e808a3b8065b43f047b409e4a3f.gif)