Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limity, asymptoty a monotonie (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 02. 2016 00:43
Limity, asymptoty a monotonie
Dobrý den,
mám dánu funkci 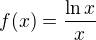 mám určit definiční obor, průsečíky s osami x a y, limity v krajních bodech def. oboru, asymptoty a vyšetřit monotonii a konvexnost, konkávnost.
mám určit definiční obor, průsečíky s osami x a y, limity v krajních bodech def. oboru, asymptoty a vyšetřit monotonii a konvexnost, konkávnost.
Celkově mě ten příklad nějak zrazuje a dost jsem se zasekla.
Řešila jsem tedy takto:
a) Definiční obor mám z podmínky  ...
... 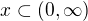 , průsečíky s osami mám:
, průsečíky s osami mám: ![kopírovat do textarea $[0,0]$](/mathtex/65/65b6edb92cc4ce515fc6a70a1d2d277d.gif) a
a ![kopírovat do textarea $[1,0]$](/mathtex/91/91a3ccdf14346c86322c0b6d2675b569.gif)
b) Limity:
Tam jsem řešila tedy  kde jsem použila l'Hosp. pravidlo a dostala jsem se na
kde jsem použila l'Hosp. pravidlo a dostala jsem se na  . Dále jsem dala že
. Dále jsem dala že 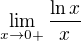 a vyšlo mi
a vyšlo mi  . Pro
. Pro 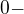 nemá cenu řešit, není definováno, je tak?
nemá cenu řešit, není definováno, je tak?
c) Asymptoty jsem řešila podle vzorce: 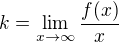 a
a 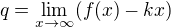 , obě mi vyšly
, obě mi vyšly 
d) Při řešení stacionárních a inflexních bodů jsem ale narazila na to, že tam žádné nejsou, první a druhá derivace mi výjde s podmínkou že  se nerovná
se nerovná  a nula není v definičním oboru...
a nula není v definičním oboru...
To, k čemu jsem se dopočítala v předchozích bodech tím si také nejsem jistá a u těch extrémů opravdu nevím co dělám špatně, ale příjde mi to opravdu divné.
Moc děkuji za pomoc :) budu vděčná.
Offline
- (téma jako vyřešené označil(a) TerezaG)
#2 16. 02. 2016 00:57
Re: Limity, asymptoty a monotonie
a) jak může být průsečíkem bod ![kopírovat do textarea $[0,0]$](/mathtex/65/65b6edb92cc4ce515fc6a70a1d2d277d.gif) , když je
, když je 
b) limita pro 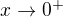 je špatně
je špatně
c) ok
d) asi máš špatně spočítané derivace, protože jak extrém tak inflexe existují
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 16. 02. 2016 12:03
Re: Limity, asymptoty a monotonie
Offline
#7 16. 02. 2016 12:06
#8 16. 02. 2016 12:11
Re: Limity, asymptoty a monotonie
↑ TerezaG:
Zdravím,
já se vrátím k derivacím. Je zřejmé, že máš chybně zafixovaný vztah pto derivaci podílu dvou funkcí:
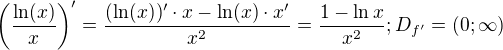
Offline
#10 16. 02. 2016 12:28 — Editoval Rumburak (16. 02. 2016 13:18)
Re: Limity, asymptoty a monotonie
↑ TerezaG:
V případě 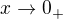 by "neurčitými výrazy" byly např.
by "neurčitými výrazy" byly např.
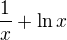 (typu
(typu  ) nebo
) nebo 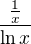 (typu
(typu 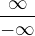 čili
čili 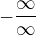 ) ,
) ,
kde si obě nekonečna navzájem "konkurují".
Avšak v typech  resp.
resp. 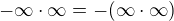 obě nekonečna "spolupracují",
obě nekonečna "spolupracují",
takže o neurčité výrazy nejde.
Offline
#11 16. 02. 2016 12:30
#14 16. 02. 2016 12:42
Re: Limity, asymptoty a monotonie
↑ TerezaG:
Stacionární body - vyšetřuji pvní derivaci a ptám se, kdy je rovna nule.
Inflexní body - vyšetřuji druhou derivaci a ptám se, kdy je rovna nule.
Offline
#16 16. 02. 2016 13:40
Re: Limity, asymptoty a monotonie
↑ TerezaG:
Co Ti nehraje ?
Máme funkci
(1)  .
.
Najít stacionární body funkce  obecně znamená vyřešit rovnici
obecně znamená vyřešit rovnici
(2) 
pro neznámou  . Symbol
. Symbol 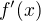 značí derivaci funkce
značí derivaci funkce  v bodě
v bodě  patřícím samozřejmě do definičního oboru
patřícím samozřejmě do definičního oboru
jak funkce  , tak i její derivace
, tak i její derivace 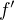 .
.
Jak bude vypadat rovnice (2) pro funkci (1) ?
Offline
#17 16. 02. 2016 14:08
#18 16. 02. 2016 14:18 — Editoval Al1 (16. 02. 2016 14:22)
Re: Limity, asymptoty a monotonie
↑ byk7:
Zdravím,
v příspěvku #2 s tebou nemohu souhlasit v odpovědi c): ↑ TerezaG: píše, že obě aymptoty jí vyšly 0. Jenže ona počítá jen parametry asymptoty se směrnicí ( ty opravdu vycházejí oba rovny 0) - rovnice asymptoty je y=0. Neřeší ( a ani ty) asymptotu bez směrnice.
Offline
#19 16. 02. 2016 14:19
#22 16. 02. 2016 14:34
Re: Limity, asymptoty a monotonie
↑ TerezaG:
Ano.
Teď ještě ověřit, zda se jedná o extrém.
Navrhuji asymptoty dořešit po extrémech a inflexních bodech.
Offline
#23 16. 02. 2016 15:11
Re: Limity, asymptoty a monotonie
↑ Al1:
Dobře, takže mi vychází:
Stacionární bod  intervaly
intervaly  ... v prvním intervalu pokud jsem dosadila do první derivace f'(1)=1 ...funkce ROSTE, po dosazení z druhého intervalu f'(5)= něco záporného...funkce KLESÁ.
... v prvním intervalu pokud jsem dosadila do první derivace f'(1)=1 ...funkce ROSTE, po dosazení z druhého intervalu f'(5)= něco záporného...funkce KLESÁ.
Lokální maximum mi vyšlo po dosazení krajního bodu 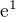 do původní funkce
do původní funkce 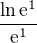 jako
jako  a to je kladné, tj jedná se o lokální MAXIMUM.
a to je kladné, tj jedná se o lokální MAXIMUM.
Druhá derivace vypadá:  z toho inflexní bod vychází
z toho inflexní bod vychází 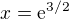
Intervaly: 
V prvním intervalu f''(1)=-3 funkce je KONKÁVNÍ
Ve druhém f''(6)= cca 0,5 což je kladné a funkce je KONVEXNÍ
Je to tak?
Offline
#24 16. 02. 2016 15:35
Re: Limity, asymptoty a monotonie
↑ Al1:
A asymptoty jsem vyřešila:
Protože je Df 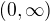 pak pro asymptotu bez směrnice řeším limitu
pak pro asymptotu bez směrnice řeším limitu  mi vychází limita nevlastní a tím pádem existuje asymptota
mi vychází limita nevlastní a tím pádem existuje asymptota  je to tak??
je to tak??
Ty další se směrnicí už jsem vyřešila předtím. Jsou nulové
Offline
#25 16. 02. 2016 15:53
Re: Limity, asymptoty a monotonie
↑ TerezaG:
Extrémy:![kopírovat do textarea $[e, e^{-1}]$](/mathtex/c8/c867de7f08c8da76bed857de4823bcd8.gif) je lokální maximum, ale ne proto, že (cituji):"
je lokální maximum, ale ne proto, že (cituji):" a to je kladné, tj jedná se o lokální "MAXIMUM.
a to je kladné, tj jedná se o lokální "MAXIMUM.
Pro zhodnocení extrémů máš dvě možnosti:
1.jestliže v levém okolí stacionárního bodu je fce rostoucí a v pravém klesající, pak je v tomto bodě lokální maximum (jeho hodnota může být klidně záporná, fce 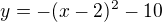 má maximum v bodě
má maximum v bodě ![kopírovat do textarea $[2; -10]$](/mathtex/cc/cc83c3f9484dc5db5f80bec11717e1a4.gif) a -10 je záporné),
a -10 je záporné),
jestliže v levém okolí stacionárního bodu fce klesající a v pravém rostoucí, pak je v tomto bodě lokální minimum.
2. nebo užiješ druhou derivac a dosadíš x stacionárního bodu.Zde druhá derivace je v bodě záporná - lokální maximum, pokud je kladná-lokální minimum
druhá derivace je v bodě záporná - lokální maximum, pokud je kladná-lokální minimum
Ještě také: já asi vím, jak jsi určovala, kdy je první ( i druhá derivace) kladná či záporná, ale jen z toho, že f'(1)=1 nebo
f''(1)=-3 neplyne, že je fce rostoucí (konkávní v intervalu). Zde spíše jen napiš, že nerovnice řešíš metodou nulových bodů
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limity, asymptoty a monotonie (TOTO TÉMA JE VYŘEŠENÉ)

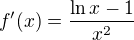 jako podíl.
jako podíl.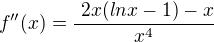 . Není to správně?
. Není to správně? , kde pro
, kde pro 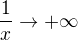 ,
,  .
.  ?
?
