Matematické Fórum

holyduke · 07. 03. 2016 18:25

Ahoj,
mějme funkci $f(x,y,z)=x^{2}+yz$ a mám určit derivaci v bodě $[1,2,-1]$ ve směru vektoru $\vec{s}=(-1,1,2)$ .

Moje otázka je, změnilo by se něco kdyby byl vektor $\vec{s}=(-2,2,4)$ ? Podle profesorova výkladu ano, ale mně to logiku nedává. Přece směr těchto vektorů je stejný, tím pádem i derivace by měla být stejná, ne?

Jj · 07. 03. 2016 20:18

↑ holyduke:

Dobrý den.

Řekl bych, že pokud profesor nedefinoval derivaci ve směru výhradně s jednotkovým směrovým vektorem, tak má pravdu.

Pokud vím, tak tato definice nebyla jednotná a podle uvedeného je tomu tak asi dosud.

holyduke

↑ Jj:
Ale sklon těchto tečen je přece stejný ne? Takže podle mě i derivace musí být stejné. Rozumím tomu takhle:

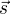V tomto případě vyjde $\varphi '(t)=1$ a to chápu tak, že je to hodnota diferenciálu, kde přírůstek na ose je velikost vektoru $\vec{s}$ . Tím pádem velikost tohoto diferenciálu bude závislá právě na velikosti vekoru 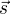$\vec{s}$ , ale pokud to podělím a udělám tangens (=derivaci), tak mi vždy vyjde stejné číslo (=stejný sklon vzhledem k půdorysně).

Takže vlastně chápu pojem derivace ve směru stejně jako diferenciál funkce jedné proměnné.

Chápu to správně nebo jsem mimo?

Rumburak

↑ holyduke:

Ahoj.

Jak už naznačil kolega ↑ Jj:, závisí to ne na intuitivní geometrické úvaze o sklonu jakési tečny, ale na
přesné definici pojmu "derivace funkce ve směru". Já ji znám takto :

$f'_{\vec{u}}(A) := \lim_{h \to 0}\frac{f(A+h\vec{u}) - f(A)}{h}$

(derivace funkce $f$ v bodě $A$ ve směru vektoru $\vec{u}$ , pokud tato limita podle reálné proměnné $h$ existuje).
Snadno nahédneme, že podle této definice je např. $f'_{t\vec{u}}(A) = t f'_{\vec{u}}(A)$ pro reálné $t$ , pokud existuje
limita vpravo.