Matematické Fórum

krauva · 12. 03. 2016 17:14

Ahojte,
potřeboval bych pomoct s jedním příkladem, výsledku jsem se dopočítal, ale zdá se mi nesprávný a nemůžu najít chybu:
Jsou dána soustava 2 rovnic: $2x^3-y^2-1=0 \wedge xy-y-4=0$ Mám nalézt první aproximaci z počátečního bodu [1,2]

Určil jsem si první derivace: $\frac{\partial f1}{\partial x} = 6x^2$ ; $\frac{\partial f1}{\partial y} = -2y$ ; $\frac{\partial f2}{\partial x} = y$ ; $\frac{\partial f2}{\partial y} = x-1$
Jakobiho matice v (x0, y0) je: $\begin{pmatrix} 6 \ -4 \\ 2 \ \ \ \ \ 0\\ \end{pmatrix}$
a funkční hodnota v (x0, y0) je (-3,-4)

řeším pak: $\begin{pmatrix} 6 \ -4 \\ 2 \ \ \ \ \ 0\\ \end{pmatrix}$ $\begin{pmatrix} \triangle x\\ \triangle y\\ \end{pmatrix}$ = - $\begin{pmatrix} -3\\ -4\\ \end{pmatrix}$
z toho mi vychází $x1 = x0+ \triangle x = 3 \wedge y1 = y0 + \triangle y = \frac{17}{4}$
když ale tyto hodnoty dosadím do původní rovnice, tak se více vzdalují od nuly než původní nultá aproximace, což by nemělo být, ne?

Děkuji za napovězení, či trknutí

jelena · 13. 03. 2016 11:40

Zdravím,

pokud jsem neudělala chybu při derivování a dosazování, potom výsledek mám stejně. Když se podívám na hledaný průsečík zadaných křivek, tak nalezený bod je mu blíž, než původní (1, 2) - můžeš počítat kontrolu přes vzdálenost bodů. Zde mám něco málo ohledně počátečního bodu i s odkazem od kolegy na příklad. V tomto konkrétním případě bych také vyjadřovala y=f(x) z druhé funkce a při návrhu počátečního bodu bych vycházela z některého bodu na této křivce.
Vy máte počáteční bod zadaný, v postupu chybu nevidím, k možné interpretaci výsledku snad ještě přidá někdo z kolegů. Děkuji.

krauva · 13. 03. 2016 18:54

Díky za kontrolu. Zdá se mi je divné, že když dosadím nulté aproximace do rovnic, tak dostanu -3 a -4. A když dosadím první aproximace, tak obdržím 34,9 a 4,5 – obě čísla jsou (v absolutní hodnotě) dál od nuly. Takže tohle není určující?

jelena · 13. 03. 2016 20:11

↑ krauva:

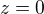v odkazu v ↑ příspěvku 2: povídám, jak si představuji použití jednotlivých bodů. Zápis $2x^3-y^2-1=0$ rozumím buď funkci v rovině xOy zadanou implicitně nebo funkci 2 proměnných f(x, y), která v prostoru tvoří plochu a tuto plochu jsme řízli rovinou $z=0$ a máme proto křivku v rovině $2x^3-y^2-1=0$ . Když do předpisu $f(x,y)=2x^3-y^2-1$ dosazuji hodnoty souřadnic bodu (x, y) dostávám bod v prostoru na ploše $f(x,y)=2x^3-y^2-1$ . Že ten bod nějak vzdálen od roviny xOy záleží jen na samotném předpisu funkce $f(x,y)=2x^3-y^2-1$ a nemá souvislost s tím, jak daleko projekce tohoto bodu do roviny xOy vzdálena od průsečíku křivek. Tento průsečík hledáme jako řešení soustavy rovnic a zajímá nás jak dobře se k němu blížíme při hledání.
Obdobně můžeme diskutovat i ve vztahu k druhé funkce, je to mé odůvodnění, proč výsledek dosazování nemá souvislost s úspěšnosti řešení. Alespoň tak si představuji, ale budu vděčná za kvalifikovanější pohled kolegů, kolegům děkuji.

krauva · 13. 03. 2016 20:28

↑ jelena:
Jo, to máš pravdu. Teď si to už lépe představím. Díky moc...

Matematické Fórum

#1 12. 03. 2016 17:14

Newtonova metoda – 2 rovnice o 2 neznámých

#2 13. 03. 2016 11:40

Re: Newtonova metoda – 2 rovnice o 2 neznámých

#3 13. 03. 2016 18:54

Re: Newtonova metoda – 2 rovnice o 2 neznámých

#4 13. 03. 2016 20:11

Re: Newtonova metoda – 2 rovnice o 2 neznámých

#5 13. 03. 2016 20:28

Re: Newtonova metoda – 2 rovnice o 2 neznámých

Zápatí