Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 03. 2016 16:25
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
lineárna homogénna diferenciálna rovnica
zdravím, ako mam riesit tuto rovnicu LHDR (t je nezavisla premenna, x závisla), pomocou metodou variácie konštanty, kedze t potrebujem nejak vyňat spod derivácie x'.
rovnica : 
a mame to riesit tak, ze najprv najdeme riesenie bez pravej strany, kde prava strana je nejaka funkcia t, a potom partikulárne riesenie so závislou premennou C.
Tak ja fakt neviem, ako mam to upravit. Dik za hocijaku radu.
Offline
#2 13. 03. 2016 17:22
Re: lineárna homogénna diferenciálna rovnica
↑ miso16211:
Dobrý den.
Řekl bych, že i když je ' t ' nezávislá proměnná, tak bych u této rovnice hledal řešení právě 'naopak', tzn. x jako nezávislá. Pak by úprava byla 
Což je nehomogenní lineární diferenciální rovnice pro funkci t(x) (jinou úpravu zadané rovnice si nějak neumím představit).
Pak homogenní rovnice bude , jejím řešením dostanete funkci
, jejím řešením dostanete funkci 
Variace konstanty: --> po dosazení za t':
--> po dosazení za t':
takže 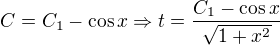
Pokud se tedy nemýlím.
Offline
#3 14. 03. 2016 19:22
#4 14. 03. 2016 22:31
Re: lineárna homogénna diferenciálna rovnica
↑ miso16211:
Ano, může se to a některé školní příklady tento postup i předpokládají (tento asi taky - je zřejmé, že při řešení vše hezky školně do sebe zapadá, a jiným způsobem z toho těžko vykouzlíte lineární diferenciální rovnici).
Není to 0. Je to to, co je napsáno - tedy dt/dx, místo funkce x(t) najdete jako řešení diferenciální rovnice funkci t(x). Pokud tato splňuje diferenciální rovnici, je to v pořádku. Z řešení je zřejmé, že funkce x(t) se ani nedá vyjádřit pomocí elementárních funkcí.
Pokud se tedy nemýlím.
Offline
