Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 05. 03. 2009 20:38
Re: Kvadratická rovnice
↑ Alivendes:
Je viac metod ako to jednoducho urobit :) Jedna moznost je podla znameho vzorca, ja ukazem dve dalsie. Prva je s vyuzitim tzv. Vietovych vztahov, ktore hovoria ze ak mame kvadraticku rovnicu  , tak pre jej korene
, tak pre jej korene  plati:
plati:  a
a  . Skusime konkretny priklad:
. Skusime konkretny priklad:
Mame rovnicu  . Hladame teda korene tak, aby ich sucet bol
. Hladame teda korene tak, aby ich sucet bol  a sucin
a sucin  . Velmi lahko sa da prist na to, ze tieto korene budu (-5) a (-3). No a nakoniec vyuzijeme, ze kazda kvadraticka rovnica (vo vyssie uvedenom tvare) sa da napisat v tvare
. Velmi lahko sa da prist na to, ze tieto korene budu (-5) a (-3). No a nakoniec vyuzijeme, ze kazda kvadraticka rovnica (vo vyssie uvedenom tvare) sa da napisat v tvare  , z coho po dosadeni korenov dostavame pre nasu rovnicu tvar
, z coho po dosadeni korenov dostavame pre nasu rovnicu tvar  , po uprave
, po uprave  . Po roznasobeni zistime, ze sme dostali naozaj povodnu rovnicu.
. Po roznasobeni zistime, ze sme dostali naozaj povodnu rovnicu.
Druha metoda ktoru opisem sa nazyva metoda doplnenim na uplny stvorec. Vezmeme prve dva cleny kvadratickej rovnice a doplnime treti clen tak, aby sme mohli pouzit vzorec. Radsej to skusme ukazat na priklade z prvej metody. Vezmeme teda cleny  . Aby sme mohli pouzit vzorec
. Aby sme mohli pouzit vzorec  , tak musime zrejme doplnit cislo 16. Samozrejme nasledne ho musime aj odpocitat, aby sa rovnost zachovala. Teda:
, tak musime zrejme doplnit cislo 16. Samozrejme nasledne ho musime aj odpocitat, aby sa rovnost zachovala. Teda:  . Teraz mozme vyuzit dalsi vzorec:
. Teraz mozme vyuzit dalsi vzorec:  . Na pravej strane rovnice bola nula, takze mame
. Na pravej strane rovnice bola nula, takze mame  .
.
Odporucam precvicit tieto metody napriklad na rovniciach  ,
,  a
a  . Vysledky mozes napisat aj sem, niekto urcite skontroluje :)
. Vysledky mozes napisat aj sem, niekto urcite skontroluje :)
Offline
#5 05. 03. 2009 21:35
Re: Kvadratická rovnice
↑ Alivendes:
Nie je za co :) Ale ak Ti mozem poradit tak naozaj si to vyskusaj na prikladoch :)
Offline
#8 05. 04. 2009 13:17 — Editoval joker (05. 04. 2009 13:20)
#10 09. 04. 2009 12:32
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Kvadratická rovnice
muzete mi nikdo zkontrolovat tento příklad:
rozložte kvadratický trojčlen: 
...me vyslo 
...ale vysledek ma vyjit 
Offline
#11 09. 04. 2009 12:39 — Editoval Cheop (09. 04. 2009 12:40)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Kvadratická rovnice
↑ vonSternberk:
Zkus si ten svůj výsledek zpětně roznásobit
Dostaneš:
Zadání však je: proto
proto 
Nikdo není dokonalý
Offline
#12 09. 04. 2009 12:42
Re: Kvadratická rovnice




Máš to správně,až na jednu ,,velkou nepřesnost,každou kvadratickou rovnici můžeš psát ve tvaru: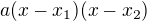
A protože už z šesté třídy víme,že mínus a mínus nám dá plus,proto to musíš napsat takto:
( :)
:)
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#14 21. 04. 2009 20:06
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Kvadratická rovnice
chci se zeptat co mám udělat, když mi vyjde diskriminant 0?
Offline
#15 21. 04. 2009 21:10
- marnes

- Příspěvky: 11227
Re: Kvadratická rovnice
↑ vonSternberk:Pak máme jen jedno řešení - jeden kořen - někdy též nazývaný dvojnásobný x = -b/2a
Jo. A na začátku vás zdravím.
Offline


 a
a 









