Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 04. 2016 12:55
Pravděpodobnost. Binomické rozdělení
Dobrý den, jak bych měl řešit toto:
Dva basketbalisti mají po třech hodech na koš. První zasáhne koš při každém hodu s pravděpodobností 0,6, druhý s pravděpodobností 0,7. Určete pravděpodobnost, že po všech šesti hodech budou mít oba stejný počet zásahů.
___
Není mi jasné, jestli ty prvotní 3 pokusy mám nějak zohledňovat nebo je brát jako hotovou věc...
Řešil bych to takto:
( 6 nad x ) * 0,6^x * (1-0,6)^(6-x) = ( 6 nad x ) * 0,7^x * (1-0,7)^(6-x)
Z cehoz zjistim kolik je to stejne mnozstvi zasahu. (vyslo mi 3,9 -> takze 4?)
A nasledne z leve nebo prave strany po dosazeni x vyjadrim pst techto 4 zasahu. To mi vyslo 0,0995.
Co si o tom myslite? Diky.
Offline
#2 03. 04. 2016 13:33
Re: Pravděpodobnost. Binomické rozdělení
↑ Mythic:
Zdravím.
X1, X2 = počet zásahů prvního, druhého (náhodné proměnné) v jeho třech hodech
Řekl bych, že
Zásahy jednoho jsou nezávislé na zásazích druhého
Takže hledaná pravděpodobnost (tj. oba mají shodně 0 nebo 1 nebo 2 nebo 3 zásahy) bude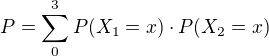
Pokud se tedy nemýlím.
Offline
