Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Geometrické rozdělení (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 04. 2016 15:48
Geometrické rozdělení
Mohli byste mi prosím vysvětlit tento příklad?
Dva hráči střídavě házejí kostkou. Vyhrává ten, kdo první hodí šestku. Jaká je pravděpodobnost, že vyhraje ten, který začínal?
Z výsledků vím toto:
p-úspěchu: 1/6
p-neúspěchu: 5/6
výsledke: =(1/6)*(1/(1-(5/6)^2))
Bohužel ale moc nechápu úvahu v pozadí. :/ Díky!
Offline
- (téma jako vyřešené označil(a) Mythic)
#2 03. 04. 2016 17:50
Re: Geometrické rozdělení
↑ Mythic:
Úvahu bych viděl zhruba takto:
p = 1/6, q = 5/6, N = pořadí vyhrávajícího tahu (náhodná proměnná).
Má-li vyhrát začínající hráč, tak musí být hra ukončena v libovolném lichém tahu --> najít pravděpodobnost 
Pravděpodobnost P(N= právě 2n+1) pro nezáporné celé n je podle geometrického rozložení 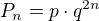 ,
,
a hledaná pravděpodobnost bude tudíž 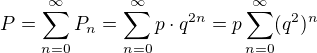 , takže bude součtem uvedené geomegtrické posloupnosti:
, takže bude součtem uvedené geomegtrické posloupnosti:
Pokud se tedy nemýlím.
Offline
#4 09. 06. 2016 18:11 Příspěvek uživatele Mythic byl skryt uživatelem Mythic.
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Geometrické rozdělení (TOTO TÉMA JE VYŘEŠENÉ)
