Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Projekt "Matematika s radostí"
#51 06. 01. 2014 13:35
- petr_beremlijski

- Zelenáč
- Příspěvky: 15
- Reputace: 2
Re: Projekt "Matematika s radostí"
↑↑ Jan Jícha:↑↑ Jan Jícha:Chybný odkaz jsem opravil. Děkuji za upozornění. Připomínky ke grafické podobě jsem předal tvůrci našeho webu. :-) Děkuji, Petr Beremlijski
Offline
#52 06. 01. 2014 14:27
- petr_beremlijski

- Zelenáč
- Příspěvky: 15
- Reputace: 2
Re: Projekt "Matematika s radostí"
↑↑ Kondr:Děkuji za připomínky. Pokusíme se je projít. Materiály samotné jsou volné (jde o materiály vytvořené v projektu OP VK).
Offline
#53 06. 01. 2014 14:34
- petr_beremlijski

- Zelenáč
- Příspěvky: 15
- Reputace: 2
Re: Projekt "Matematika s radostí"
↑↑ jelena:Nerozumím, v čem má být nejednoznačnost. Monotonie přece není definována pomocí pojmu derivace.
Časovou náročnost testů neodhadujeme, ale záměrem je vytvářet takové testy, aby byly použitelné i časově při výuce.
Offline
#54 06. 01. 2014 14:37
- petr_beremlijski

- Zelenáč
- Příspěvky: 15
- Reputace: 2
Re: Projekt "Matematika s radostí"
↑↑ Peta8:Od začátku roku 2013 (ale to na něm téměř ještě nic nebylo) má zatím 3276 unicitních návštěvníků, kteří si zobrazili 33247 stránek.
Offline
#55 07. 01. 2014 15:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Projekt "Matematika s radostí"
↑ petr_beremlijski:
děkuji :-) jen se ptám, jak se s radosti (a nejen) zapíší intervaly monotonnosti těchto funkcí: 
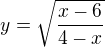 . Nijak to nespěchá, děkuji.
. Nijak to nespěchá, děkuji.
Offline
#56 07. 01. 2014 17:15 — Editoval kaja.marik (07. 01. 2014 17:15)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Projekt "Matematika s radostí"
↑ jelena:Pekny den. To je asi obecna otazka. Jak to je v projektu nevim, ale jestli je otazka minena tak, ze jedna z odpovedi 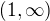 a
a  je spatne, tak to je podle mne spis opodstatnele jenom v pripade, ze je v otazce presne uvedena definice monotonie ktera se ma pouzit a neni to test z matematiky ale z logiky. Mam za to, ze rozumny vyucujici vi, ze v ruznych materialech to je jinak (nekdo uvazuje monotonii jenom na otevrene mnozine, nekdo na obecne) a uzna kteroukoliv, protoze pouzivani materialu i od jinud je plus a znaci zvidaveho ducha.
je spatne, tak to je podle mne spis opodstatnele jenom v pripade, ze je v otazce presne uvedena definice monotonie ktera se ma pouzit a neni to test z matematiky ale z logiky. Mam za to, ze rozumny vyucujici vi, ze v ruznych materialech to je jinak (nekdo uvazuje monotonii jenom na otevrene mnozine, nekdo na obecne) a uzna kteroukoliv, protoze pouzivani materialu i od jinud je plus a znaci zvidaveho ducha.
Offline
#57 07. 01. 2014 17:18
- petr_beremlijski

- Zelenáč
- Příspěvky: 15
- Reputace: 2
Re: Projekt "Matematika s radostí"
↑ jelena:První funkce je dle mého názoru rostoucí v  a druhá funkce je klesající v
a druhá funkce je klesající v 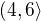 .
.
Offline
#58 08. 01. 2014 00:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Projekt "Matematika s radostí"
↑ kaja.marik:, ↑ petr_beremlijski:
Zdravím a děkuji,
otázka je míněna tak, že jsem se ptala v předchozích příspěvcích, zda je referenční teoretický materiál (např. si představuji Poláka, nebo, jak uvádí pan Petr Kovář sadu Matematiky pro gymnázia).
V tématu ohledně monotonie funkce jsem zrovna narazila na situaci, kdy jen z definice jsem neuměla vyvrátit (nebo potvrdit), že výsledek v Petákové obsahuje překlep (má 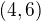 , nebo, že jen rozdíl v definici + příspěvek 7 stejného tématu.
, nebo, že jen rozdíl v definici + příspěvek 7 stejného tématu.
Ale zrovna v tomto cvičení ve výsledcích asi překlepy budou (napr. 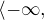 ).
).
rozumny vyucujici vi
:-) samozřejmě, ale testy v projektu vyhodnocuje stroj, tak proto by ten referenční materiál byl vhodný (ale zas kontrolovat, aby i v dalších edicích souhlasil s projektem - sama potíž z toho).
Offline
#59 12. 01. 2014 02:10
#60 12. 01. 2014 10:13 — Editoval jelena (10. 03. 2014 22:44)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Projekt "Matematika s radostí"
↑ Jan Jícha:
Ještě zdravím,
myslím, že označení 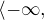 nejde použit ani pro R, používáme jen (-oo,... nebo +oo). Tedy otevřený interval. Tento "překlep" mne vedl na domněnku, že i v jiných výsledcích může být překlep.
nejde použit ani pro R, používáme jen (-oo,... nebo +oo). Tedy otevřený interval. Tento "překlep" mne vedl na domněnku, že i v jiných výsledcích může být překlep.
V Polákovi starší vydání (1976) je definice stejná, ale potom mi není jasné, že má (cituji) "funkce  je klesající v intervalu (-oo, 0>, neboť pro všechna
je klesající v intervalu (-oo, 0>, neboť pro všechna  je
je  " (vždyt to neplatí pro samotnou 0, tedy interval by měl být otevřený i v 0).
" (vždyt to neplatí pro samotnou 0, tedy interval by měl být otevřený i v 0).
To je spíš ukázka, že referenční teoretický materiál je dobré mít jednoznačně a dosažitelně.
Edit: v zápisu  bylo přehozeno znaménko, opraveno v příspěvku.
bylo přehozeno znaménko, opraveno v příspěvku.
Offline
#61 10. 03. 2014 14:13 — Editoval oldrich.vlach (10. 03. 2014 14:14)
- oldrich.vlach
- Zelenáč
- Příspěvky: 6
- Reputace: 0
Re: Projekt "Matematika s radostí"
↑ jelena:
Dobrý den,
moc nerozumím textu v závorce
(vždyť ...)
Dle linkované definice monotonie funkce na intervalu, je tvrzení:
funkce 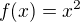 je klesající v intervalu
je klesající v intervalu  , neboť
, neboť  je
je 
pravdivé. Nula (krajní bod intervalu) nečiní problém. Jediná chyba tam byla ve znaménku při porovnávání funkčních hodnot
Offline
#62 10. 03. 2014 22:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Projekt "Matematika s radostí"
↑ oldrich.vlach:
Zdravím Vás,
ohledně znamének > < jsem měla překlep, opraveno. Ale já mám (z Poláka) pro uzavřený interval  před 0 znaménko
před 0 znaménko  tak (
tak ( ) a proto říkám, že pro 0 to neplatí.
) a proto říkám, že pro 0 to neplatí.
A Vy máte před 0 znaménko 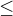 tak
tak  , tak u Vás platí. Proto se ptám, zda je správné posuzovat i krajní bod intervalu, nebo mít interval otevřený a je po debatách?
, tak u Vás platí. Proto se ptám, zda je správné posuzovat i krajní bod intervalu, nebo mít interval otevřený a je po debatách?
---------------
OT: pozoruji, že byla zavedená nová možnost přispívání na provoz plácku :-) Ale zaktualizovat Manuál, to nic.
Offline
#63 10. 03. 2014 23:20
Re: Projekt "Matematika s radostí"
Pozdravujem ↑ jelena:,
Vo vela matematickych co poznam, monotonne funkcie su definovane na nejakom intervale I, bez toho aby bolo upresnene nieco o nom.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#64 10. 03. 2014 23:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Projekt "Matematika s radostí"
↑ vanok:
Také zdravím,
šlo o to, jak zapsat interval monotonie pro funkce:
1. 
2. 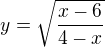
↑ viz příspěvek 58: V písemné práci není problém napsat komentář, případně své zdůvodnění obhájit (nebo neobhájit). Ale v testu s možnosti volby si tak mohu způsobit zbytečnou chybu - jen pro jemné rozdíly v definici.
Offline
#65 10. 03. 2014 23:31 — Editoval vanok (11. 03. 2014 00:39)
Re: Projekt "Matematika s radostí"
↑ jelena:
Skutocne, to si dobre videla, ze som necital cele vlakno.
V takom pripade by som bral ten najvadci mozny.
1) odpoved: striktne monotonna na 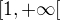
2) odpoved: je striktne monotonna na kazdom z inervalov ![kopírovat do textarea $]-\infty, 4[$](/mathtex/f1/f12fe69f48bbbc019bb869f99d2c7546.gif) ;
; 
Poznamka: niekto sa moze zmylit v odpovedi, au pouzije vetu o znamienku derivacie kazdej z funkcii. ( a tak, implicitne predpoklada ze sa zaujimame o vsade derivantelne funkcie...co tu neplati)
Monotonnost sa tu da vysetrit aj inac
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#66 11. 03. 2014 14:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Projekt "Matematika s radostí"
↑ vanok:
Zdravím a děkuji, celá debata vznikla, že jsem se ptala na "referenční teorii" ↑↑ jelena: (jelikož si myslím, že u tak rozsáhlého testovacího projektu je to dobré mít).
Offline
#67 11. 03. 2014 15:11
Re: Projekt "Matematika s radostí"
↑ jelena:
Pozdravy, tak aspon dufam, ze som pomohol vyjasnit situaciu.
A tiez poukazat na nebezpecie, ze pouzit nejaku teoremu bez pozozneho overenia hypotez nemoze dat ( skoro nikdy) dobru odpoved, a nikdy platny dokaz.
Iste to ma aj suvis z dobrou redakciou.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#68 13. 03. 2014 13:20
- oldrich.vlach
- Zelenáč
- Příspěvky: 6
- Reputace: 0
Re: Projekt "Matematika s radostí"
↑ jelena:
Dobrý den, omlouvám se za reakci až nyní, moc sem nechodím.
Poláka bohužel neznám a bral jsem tedy definici z Vašeho odkazu na wikipedii. Ta říká přesně to, co jstem tam měl napsáno (otázka na ostré/neostré znaménko nerovnosti).
Offline
#69 14. 03. 2014 00:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Projekt "Matematika s radostí"
↑ oldrich.vlach:
děkuji, ale pořád v tomto zápisu
wikipedie napsal(a):
Monotonie globální (na intervalu):
Funkce je na intervalu I rostoucí, jestliže pro všechnaz tohoto intervalu platí:
.
a obdobně pro klesající. Pro všechna x menší y z tohoto intervalu (tedy i pro 0 menší čeho z tohoto intervalu?). Pořád mluvíme o intervalu  .
.
moc sem nechodím... Poláka bohužel neznám
:-) kolega Rumburak také tvrdil, že odmaturovat z ČJ jde bez čtení díla Karolíny Světlé, tak abyste sem nechodil častěji a budu Vám pročítat nejlepší místa z Poláka (jako kolegovi). Mám výborný tisk ze začátku 70. let.
Zpět k problému - věřím, že v projektu bude zařazen test pro vyšetření monotonie (zatím nevidím), tak ho vyplním a porovnám definice. To bude asi nejvíce průkazné. Zdravím Vás a kolegy.
Offline
#70 16. 04. 2016 21:38
Re: Projekt "Matematika s radostí"
↑↑ petr_beremlijski: Já to otevřel v Adobe readru a stejně to nejde.
Offline
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Projekt "Matematika s radostí"