Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 04. 2016 10:50 — Editoval Statistik (20. 04. 2016 10:54)
obor konvergencie
Ahojte, mam takuto ulohu:
Najdite obor konvergencie radu 
no obor konvergencie je vlasne taka mnozina  bodov
bodov  ze plati
ze plati  to mam z definicie oboru konvergencie. Takze podla mna bude obor konvergencie
to mam z definicie oboru konvergencie. Takze podla mna bude obor konvergencie 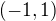 lebo ak v rade
lebo ak v rade  za n-ko budem dosadzovat cisla tak rad konverguje len v pripade ze
za n-ko budem dosadzovat cisla tak rad konverguje len v pripade ze  co poviete, mam to dobre alebo som mimo?
co poviete, mam to dobre alebo som mimo?
Offline
#2 20. 04. 2016 11:34
- Eratosthenes
- Příspěvky: 2936
- Reputace: 139
Re: obor konvergencie
ahoj ↑ Statistik:,
není to dobře. n je index členů řady, takže je vždycky n = 1;2;...;1000;.... (nekonečno -:). Asi tě zmátlo značení v té vaší definici - ta mimochodem k řešení není použitelná, protože mluví o mocninné řadě a zadaná řada mocninná není. Máš zjistit, pro která x řada konverguje (nikoliv pro která n...)
Budoucnost patří aluminiu.
Offline
#4 20. 04. 2016 12:41 — Editoval kaja.marik (20. 04. 2016 12:42)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: obor konvergencie
Zkusil bych nejdriv specialni pripady, kde je x zaporne (a jak se n ato divam tak mozna nebude splnena nutna podminka konvergence) a kdy je x=0.
A potom mozna bude stacit se kouknout, jak se dokazuje konvergence/divergence tech rad o kterych pisete a zkusit stejny postup aplikovat na obecnou mocninu  pro kladne
pro kladne  .
.
Offline
#5 20. 04. 2016 12:43 — Editoval Statistik (20. 04. 2016 12:52)
Re: obor konvergencie
teraz som v zosite zistil pomocou D´Alembertovho porovnavajuceho kriteria, ze aj rad  diverguje.. takze aj pre
diverguje.. takze aj pre 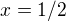 diverguje. Fakt to neviem zobecnit pre ktore konverguje a pre ktore diverguje. Je mozne ze uz pre
diverguje. Fakt to neviem zobecnit pre ktore konverguje a pre ktore diverguje. Je mozne ze uz pre  bude divergovat? Mimochodom taky rad
bude divergovat? Mimochodom taky rad  tiez diverguje Ja si myslim ze pre
tiez diverguje Ja si myslim ze pre 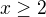 bude konvergovat a pre
bude konvergovat a pre  bude divergovat ale dokazat to neviem. Dokonca aj pre
bude divergovat ale dokazat to neviem. Dokonca aj pre  , rad
, rad  diverguje
diverguje
Offline
#6 20. 04. 2016 12:56 — Editoval kaja.marik (20. 04. 2016 12:56)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: obor konvergencie
Zkusil bych radeji integralni kriteium. Viz priklad 1.10 zde: http://mathonline.fme.vutbr.cz/download … d_file=742
Offline
#7 20. 04. 2016 12:57 — Editoval Statistik (20. 04. 2016 12:59)
Re: obor konvergencie
integralne kriterium pre ake  ? pre
? pre 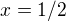 som pouzil d´alembertovo, pre
som pouzil d´alembertovo, pre  som pouzil porovnavajuce kedze
som pouzil porovnavajuce kedze  no a kedze
no a kedze  konverguje tak musia vsetky rady pre
konverguje tak musia vsetky rady pre  vacsie ako
vacsie ako 
pre  je to jasne, pre
je to jasne, pre  tiez sa daju rady porovnat. Myslim ze obor konvergencie bude
tiez sa daju rady porovnat. Myslim ze obor konvergencie bude 
Offline
#8 20. 04. 2016 13:50 — Editoval Honzc (20. 04. 2016 14:11)
Re: obor konvergencie
↑ Statistik:
Tvůj výsledek ja špatně.
Nejdříve pro x=1 dostaneme harmonickou řadu, která jak známo diverguje.
A pak integrální kritérium:


Tedy výsledek:
Řada ..... konveguje pro 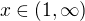
Poznámka: konvertuje se např. k islámu, ale řada konverguje.
Offline
#10 20. 04. 2016 16:26 — Editoval vanok (20. 04. 2016 16:58)
Re: obor konvergencie
Poznamka.
Rada 
( pisem  a nie
a nie  , lebo sa mi to viac paci!)
, lebo sa mi to viac paci!)
Sa vola Riemann-ova rada.
Akoze, je jasne z vlakna, ze ste uz dokazali ze pre nikoho nie je problem ukazat, ze tato rada je divergentna pre 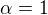 a tak aj pre vsetki
a tak aj pre vsetki 
tiez, ze je konvergentna pre  a tak pre vsetki
a tak pre vsetki  ( tento riadok sa ukaze zbytocny, ak si precitate co naslenduje)
( tento riadok sa ukaze zbytocny, ak si precitate co naslenduje)
Na doplnenie, hladanej vlasnosti nam staci ju vysetrit ze pre 
Preto je vyhodne pouzit radu vseobecneho clenu  a aplikovat Lagrange-ovu teoremu na funkciu
a aplikovat Lagrange-ovu teoremu na funkciu  na intervale
na intervale ![kopírovat do textarea $[n;n+1]$](/mathtex/e9/e93fd04f354160b441d7e36c7cd31802.gif) .....
.....
Z tymto iste dokazete ukoncit hladany dokaz( alebo si precitajte vase poznamky z prveho rocnika VS)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 diverguje ale napr.
diverguje ale napr.  to konverguje a pre
to konverguje a pre  diverguje
diverguje