Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 05. 2016 14:39 — Editoval Rumburak (06. 05. 2016 14:48)
Re: rovnomerna konvergencia
↑ Statistik:
Ahoj.
Aby tomu bylo lépe rozumět, proveďme porovnání bodové konvergence se stejnoměrnou konvergencí,
a to nejprve u limity posloupnosti funkcí, což je z principu jednodušší..
A. Bodová konvergence. Posloupnost  koverguje k funkci
koverguje k funkci 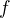 na množině
na množině  právě tehdy,
právě tehdy,
když pro každé  je
je
(0)  .
.
Zapsáno podrobněji na základě definice výroku (1) a pomocí kvantifikátorů např. :
(1)  .
.
Ve výroku (1') je "konstanta" 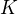 závislá nejen na
závislá nejen na  , ale také na dříve zvoleném
, ale také na dříve zvoleném 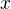 .
.
B. Stejnoměrná konvergence nastane, když 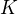 záviset na
záviset na 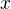 nebude, přesněji: bude-li platit silnější výrok
nebude, přesněji: bude-li platit silnější výrok
(2)  .
.
Tolik k definici stejnoměrné konvergence posloupnosti funkcí. Aplikujeme-li ji na posloupnost
částečných součtů řady funkcí, dostaneme stejnoměrnou konvergeci příslušné řady funkcí.
"Tvá" fornulace st.k. řady úplně v pořádku není. Předpoklad
konverguje
nutno nahradit předpokladem
konverguje
Stačí takto ?
Offline
#4 06. 05. 2016 15:00 — Editoval Rumburak (06. 05. 2016 15:04)
Re: rovnomerna konvergencia
↑ Statistik:
Přesně tak. Posloupnost (řada) funkcí konvergující na určité množinš stejnoměrně
konverguje i bodově (mohli bychom říci "v každém jednotlivém bodě" oné množiny),
zatímco v opačném směru to platit nemusí.
Offline
#6 06. 05. 2016 16:47
Re: rovnomerna konvergencia
↑ Statistik:
Když posloupnost (resp. řada) konverguje stejnoměrně na množině  , pak konverhule na
, pak konverhule na  i bodově,
i bodově,
jak jsme již probrali.
Příklady.
1. Posloupnost  :
:
- konverguje bodově na množině  , a sice v bodě
, a sice v bodě 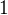 k hodnotě
k hodnotě 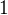 ,
,
pro ostatní  k hodnotě
k hodnotě  ;
;
- v bodech nepatřících do  je daná posloupnost divergentní;
je daná posloupnost divergentní;
- jsou-li  taková, že
taková, že  , pak na intervalu
, pak na intervalu  je konvergence
je konvergence 
stejnoměrná, protože zde  , kde
, kde  , takže
, takže
 ,
,
kde  sice závicí na
sice závicí na  , ale ne na konkretním
, ale ne na konkretním  .
.
2. Řada  konverguje na
konverguje na 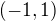 k součtu
k součtu  (jde o konkretní příklad geometrické řady).
(jde o konkretní příklad geometrické řady).
Tato konvergemce je stejnoměrná na intervalu  z předchozího odstavce, protože pro posloupnost
z předchozího odstavce, protože pro posloupnost  jejích částečných součtů platí
jejích částečných součtů platí
 ,
,
při čemž  , kde číslo
, kde číslo  (rovněž zavedené v předchozím odstavci) nezávisí na
(rovněž zavedené v předchozím odstavci) nezávisí na 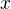 .
.
Offline

 ,
,  take, ze
take, ze  pre kazde
pre kazde  a pre kazde
a pre kazde