Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 05. 2016 19:11
Re: d´alembertovo kriterium
↑ Statistik:
Zdravím,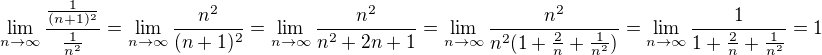
I když si nejsem jistý jestli to k něčemu bude i tak.
Offline
#4 05. 05. 2016 22:13
Re: d´alembertovo kriterium
↑ Statistik:
zkus použít kondenzační kritérium ;-)
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 06. 05. 2016 01:12
Re: d´alembertovo kriterium
Ahoj,
Preco nevyuzijes, ze  pre
pre  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 06. 05. 2016 11:15 — Editoval Rumburak (06. 05. 2016 13:47)
Re: d´alembertovo kriterium
↑ Statistik:
Ahoj.
Zdravím i ostatní účastníky diskuse.
Řada  ovšem nemá smysl, protože její člen odpovídající indexu
ovšem nemá smysl, protože její člen odpovídající indexu 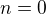 není definován.
není definován.
K rozhodnutí o konvergenci řady 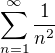 se podle mne na první pohled nabízí integrální kriterium.
se podle mne na první pohled nabízí integrální kriterium.
Offline
#7 06. 05. 2016 11:47 — Editoval jarrro (06. 05. 2016 11:47)
Re: d´alembertovo kriterium
↑ Rumburak:Ahoj. Tiež nachápem prečo je na fóre integrálne kritérium v "nemilosti"
MATH IS THE BEST!!!
Offline
#8 06. 05. 2016 12:13 — Editoval vanok (07. 05. 2016 17:16)
Re: d´alembertovo kriterium
↑ Rumburak:↑ jarrro:
Pozdravujem, mate obaja pravdu.
Ale tu ozaj staci porovnat... ( pokial pracujeme na rade bez preklepu...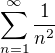 , pripade na
, pripade na  ...).
...).
Inac aj ja som za integralne kriterium!, ked d'Alembert je nerozhodny a nic ine by ma nenapadlo...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 06. 05. 2016 15:08
#12 06. 05. 2016 18:10
Re: d´alembertovo kriterium
↑ vanok:
tak složitá věc jako integrální kritérium je podle tebe vhodnější? Kondenzační kritérium dokážeš i bez analýzy a geometrickou řadu dokážeš sečíst....
Proč používat kanón na vrabce, když stačí flinta? :D
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#14 06. 05. 2016 22:14
Re: d´alembertovo kriterium
↑ Freedy:,
Najprirodzenejsie v tomto cviceni je porovnavujuce kriterium.
No kanom mozes pouzit aj na mravce, ale ...
Co je vhodne pre teba nemusi byt vhodne pre inych.....
Otazka pre teba, je vela metod na urcenie suctu tento rady, ake dokazy si uz nastudoval?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 07. 05. 2016 10:24 — Editoval Freedy (07. 05. 2016 10:35)
Re: d´alembertovo kriterium
↑ vanok:
Ahoj,
na konvergenci řady bych použil kondenzační a pak srovnání s geometrickou řadou. Obě věty jsou triviální na dokázání.
Sečíst tuto řadu sice umím, ale dokázat proč tomu tak je už ne.
Jde v podstatě o rozvoj sinu do nekonečného součinu a součtu (taylorův polynom) a poté porovnání koeficientů u x^3. Bohužel nevím, proč se sinus tomu nekonečnému součinu rovná, zřejmě asi proto, protože dle věty, kterou jsme měli, tak pokud se polynom rovná funkci v nekonečně mnoha bodech nad C, pak se ji už rovná pro všechny body C. Nicméně to je jenom heuristická úvaha.
Jinej způsob, kterej ale nevede na moc kloudný výsledek, je napsat si řadu jako mocninnou, která konverguje i pro x = 1, tedy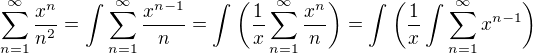
takže máme
Integrál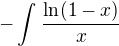
však bohužel nelze vyjádřit pomocí konečného počtu elementární funkcí.
Nicméně můžu s jistotou tvrdit (díky příslušným větám), že pokud označím 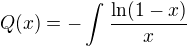
Pak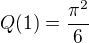
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#16 07. 05. 2016 12:45
- Eratosthenes
- Příspěvky: 2584
- Reputace: 132
Re: d´alembertovo kriterium
↑ Freedy:
No, já myslím, že 
=> konvergence
je daleko nejjednodušší.
Budoucnost patří aluminiu.
Offline
#17 07. 05. 2016 15:33 — Editoval vanok (07. 05. 2016 15:34)
Re: d´alembertovo kriterium
Poznamka.
Dam tu podrobnejsi popis dokazu o ktorom som pisal vyssie.
Najprv je jasne, ze konvergencia postupnosti 
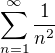 je ekvivalentna. ( cize su zaroven konvergentne alebo divergentne)
je ekvivalentna. ( cize su zaroven konvergentne alebo divergentne)
Na dokaz, ze prva rada konverguje pouzijme pre
pre 
Teraz, staci pouzit metodu "teleskopie " ... Co umozni ukoncit dokaz... Ze to vsetci dokazete!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 07. 05. 2016 15:54
Re: d´alembertovo kriterium
↑ Freedy:
Tu mas trochu historie o tej sume
https://en.m.wikipedia.org/wiki/Basel_problem
Ze je to ozaj zaujimave.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

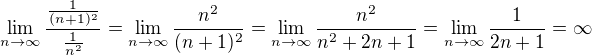 Preco mi vychadza taka blbost ze sa to rovna nekonecnu ked ten rad je konvergentny?
Preco mi vychadza taka blbost ze sa to rovna nekonecnu ked ten rad je konvergentny?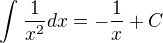 a
a  teda konverguje
teda konverguje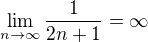 ??
??