Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 05. 2016 23:02
Lagrangeova věta
Zdravím, nejsem si úplně jistý, zda chápu výše uvedenou větu, respektive její důkaz.
Budu předpokládat, že funkce "f" splňuje předpoklady - f je spojitá na uzavřeném intervalu a,b a pro každý bod z toho intervalu existuje derivace funkce f.
Potom existuje bod 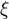 tak, že platí:
tak, že platí:
f'(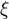 ) =
) = 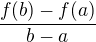
Potom si definuju nějakou funkci ![kopírovat do textarea $\psi (x) = f(x) - [\frac{f(b)-f(a)}{b-a}(x-a)+f(a)]$](/mathtex/2d/2d4cb5f7fe6770b060b87a29f733a60d.gif)
potom platí, že 
a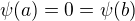
Potom podle Rolleovy věty platí, že existuje bod 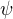 z (a,b), pro který platí, že
z (a,b), pro který platí, že 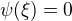
Abych řekl pravdu, tak moc nechápu tomuhle vysvětení, respektive důkazu...Nejsem si schopen nijak logicky odvodit tu moji definovanou funkci 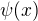 . Poprosil bych o polopatistické vysvětlení, děkuji :)
. Poprosil bych o polopatistické vysvětlení, děkuji :)
Offline
#2 15. 05. 2016 09:47
Re: Lagrangeova věta
↑ Tanner:
Ahoj
ako vo väčšine dôkazov je to nastavené tak, aby to vyšlo. Čiže zoberiem si funkciu v tvare  a z toho usúdim, že platí daná veta. Nehľadal by som v tom nejakú hlbokú logiku, je to skôr 'trik', ktorým sa dokáže daná veta.
a z toho usúdim, že platí daná veta. Nehľadal by som v tom nejakú hlbokú logiku, je to skôr 'trik', ktorým sa dokáže daná veta.
Per aspera ad astra
Offline
#3 15. 05. 2016 10:28
Re: Lagrangeova věta
Dobrý den.
Tanner napsal(a):
Potom podle Rolleovy věty platí, že existuje bod
z (a,b), pro který platí, že
Zřejmě překlep - má být 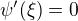
A ano, jak píše kolega, funkce 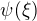 je šikovně sestavena autorem důkazu tak, že za uvedených předpokladů pro ni platí Rolleova věta - z její aplikace na tuto funkci pak jako bonus vyplyne Lagrangeova věta. Tzn., považujeme-li platnost Rooleovy věty za dokázanou, pak platí i Lagrangeova věta.
je šikovně sestavena autorem důkazu tak, že za uvedených předpokladů pro ni platí Rolleova věta - z její aplikace na tuto funkci pak jako bonus vyplyne Lagrangeova věta. Tzn., považujeme-li platnost Rooleovy věty za dokázanou, pak platí i Lagrangeova věta.
Pokud se tedy nemýlím.
Offline
#5 15. 05. 2016 19:02
Re: Lagrangeova věta
↑ vlado_bb:↑ vlado_bb:
No, obrázek právě vidím z přednášky, ale vůbec to z něj nechápu..
Offline
#11 13. 10. 2024 08:21
Re: Lagrangeova věta
Dobrý deň, nejde mi toto zadanie. Zišla by sa mu pomoc alebo aspoň napovedá.Ďakujem
Ak pre funkciu y = f(x) platí, že f(0) = (- 3) a súčasne f' * (x) <= 5 pre všetky x ∈ D(f), potom f' * (2) <= 7 Dokážte pomocou Lagrange-vej vety.
Offline
#12 13. 10. 2024 11:25
- check_drummer

- Příspěvky: 4891
- Reputace: 105
Re: Lagrangeova věta
↑ n156:
Ahoj, založ si samostatné téma. To, že se zde řešil důkaz Lagrangeovy věty neznamená, že se zde řeší i všechny její aplikace.
"Máte úhel beta." "No to nemám."
Offline
#14 19. 10. 2024 23:16
Re: Lagrangeova věta
↑ Tanner:
Ahoj
Ta věta vlastně říká, že když vezmu (f(b)- f(a))/(b-a)=tgα, tak vždy mohu sestrojit přímku, která má směrnici tgα, dotýká se té funkce v nějakém bodě, který patří do toho intervalu (a,b).
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline