Matematické Fórum

liamlim · 22. 05. 2016 10:36

Zdravím.

Mám určit, jestli je možné funkci 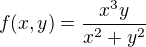$f(x,y) = \frac{x^3y}{x^2+y^2}$ spojitě dodefinovat v bodě (0,0). Vím, že většinou se toto vyvrací tak, že se blížíme po přímkách, parabolách, atd a dojdeme nějakým způsobem ke sporu. To se mi zde nepodařilo. Zkusil jsem tedy přístup:

Pro libovolné $k\ne 0$ platí $f(kx, ky) = k^2\cdot f(x,y)$ což se snadno určí dosazením. Nyní bych spočítal limitu pro $k$ jdoucí k nule, a vyšlo by mi, že funkci je možno spojitě dodefinovat v bodě (0,0) hodnotou 0. Je mi jasné, že to tak jednoduše nepůjde, proto se ptám, kde je v tomto řešení chyba.

Taky bych byl moc rád za nějaké nasměrování, jak by se tato úloha řešila správným způsobem.

Freedy · 22. 05. 2016 11:34

Ahoj,

pokud se blížíš po přímkách, tak se blížíš po přímce ve tvaru 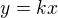$y=kx$ (když jdeš k [0,0]), případně 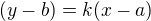$(y-b) = k(x-a)$ pro blížení k (a,b). Pak však neposíláš k k nule (k čemu?) ale x k 0. Protože pak i ypsilon jde k 0 a k ti zaručuje, že se blížíš po přímce se směrnicí k.

Tedy tvoje limita by vypadala následovně: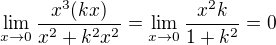
$\lim_{x\to0}\frac{x^3(kx)}{x^2+k^2x^2}=\lim_{x\to0}\frac{x^2k}{1+k^2}=0$

nicméně tímto jsi zatím nic neověřil. Pouze jsi neukázal, že neexistuje.

Limitu samotnou můžeš počítat například následujícím způsobem
Máme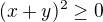
$(x+y)^2 \ge 0$ z toho dostáváme
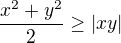$\frac{x^2+y^2}{2}\ge |xy|$ obě strany vynásobíme nezáporným číslem $x^2$
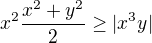$x^2\frac{x^2+y^2}{2}\ge |x^3y|$ a máme nerovnost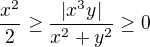
$\frac{x^2}{2}\ge \frac{|x^3y|}{x^2+y^2} \ge 0$
Nyní z věty o limitě sevřené posloupnosti dostáváme, že pravá strana jde k 0, levá taky, tedy limita jimi sevřená se rovná rovněž 0.

liamlim · 22. 05. 2016 12:16

↑ Freedy:

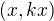Ale já jsem se přeci po žádné přímce neblížil ne? Já jsem zároveň $x$ nahradil násobkem $x$ a $y$ nahradil stejným násobkem $y$ . Nezdá se mi, že bych dosazoval například dvojici $(x,kx)$ , což vím, že správně není. Pořád moc nerozumím tomu, proč nemůžu z rovnosti

$f(kx, ky) = k^2\cdot f(x,y)$ rovnou říct, že limita pro $k$ jdoucí k nule (protože právě to mi dá na levé straně f(0,0)) je rovno nule. Ale tomu správnému řešení rozumím, velmi za něj děkuji

Freedy · 22. 05. 2016 13:01

↑ liamlim:
ano, pokud budeš zkoumat limitu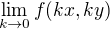
$\lim_{k\to0}f(kx,ky)$
tak se budeš blížit nulovému bodu pouze po ose první a třetího kvadrantu (oboustranně). To je dost málo k tomu, aby si něco mohl o vyšetřované limitě říct.

Těmito metodami většinou zkoumáš, jestli náhodou ta limita neexistuje. Případ kdy ti výsledná limita závisí na parametru k je nejjednodušší, protože pro různé přímky dostaneš různé limity. Případ kdy ta limita nezávisí na k (tento případ) ti nic o existenci / neexistenci limity neřekne.

Další možnost je zkoumat tuto rovnost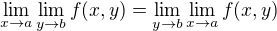
$\lim_{x\to a}\lim_{y\to b}f(x,y) = \lim_{y\to b}\lim_{x\to a}f(x,y)$
Pokud totiž nenastane, pak lze okamžitě říct, že limita neexistuje.

Matematické Fórum

#1 22. 05. 2016 10:36

Spojitost funkce více proměnných

#2 22. 05. 2016 11:34

Re: Spojitost funkce více proměnných

#3 22. 05. 2016 12:16

Re: Spojitost funkce více proměnných

#4 22. 05. 2016 13:01

Re: Spojitost funkce více proměnných

Zápatí