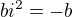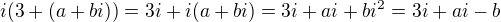Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 02. 06. 2016 16:43 Příspěvek uživatele Becrux byl skryt uživatelem Becrux.
#6 02. 06. 2016 16:45 Příspěvek uživatele Becrux byl skryt uživatelem Becrux.
#7 02. 06. 2016 16:49 — Editoval Becrux (02. 06. 2016 16:53)
#12 02. 06. 2016 17:45
- misaH
- Příspěvky: 13433
Re: Komplexné čísla
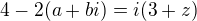
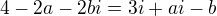
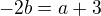 porovnané výrazy pri i (imaginárna časť)
porovnané výrazy pri i (imaginárna časť)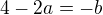 porovnané výrazy bez i (reálna časť)
porovnané výrazy bez i (reálna časť)
Offline


 na levou stranu, zbytek na pravou
na levou stranu, zbytek na pravou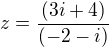 a neviem čo s tym ďalej
a neviem čo s tym ďalej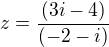 ale aj tak neviem čo s tym ďalej, skušal som ale nevychadza mi to
ale aj tak neviem čo s tym ďalej, skušal som ale nevychadza mi to
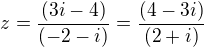
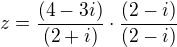
 a i(3+z) by potom bolo
a i(3+z) by potom bolo 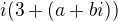 a to je
a to je  a nie
a nie 
 , proto
, proto