Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » imaginární část komplexního čísla (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 06. 2016 16:23
imaginární část komplexního čísla
Můžete mi prosím někdo poradit s tímto příkladem? Zkoušela jsem to vypočítat pomocí Moivrovy věty, k vypočítání však nesmím použít kalkulačku a bez ní si neumím poradit s třícatoutřetí mocninou..
Imaginární část komplexního čísla 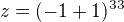 je rovna číslu:
je rovna číslu:
Offline
- (téma jako vyřešené označil(a) gadgetka)
#3 04. 06. 2016 17:24 — Editoval Waxion (04. 06. 2016 17:41)
Re: imaginární část komplexního čísla
↑ gadgetka:
Hellen to má špatně napsané.Má to být 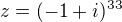
Výsledek je 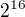
Offline
#6 04. 06. 2016 19:07
Re: imaginární část komplexního čísla
Ahoj ↑ Hellen:,
Mas vela dobrich rad od kolegov
Najst 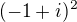 Si dokazala?
Si dokazala?
Potom 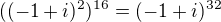
A na koniec  dokazes iste?
dokazes iste?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 04. 06. 2016 19:14 — Editoval gadgetka (04. 06. 2016 21:24)
Re: imaginární část komplexního čísla
Zdravím, a pokud můžeš počítat přes Moivreovu větu, tak kalkulačku k ničemu nepotřebuješ. Imaginární část ti vyjde 
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#9 04. 06. 2016 21:35
#12 05. 06. 2016 00:22
Re: imaginární část komplexního čísla
To se stane. Kamarádka díky kalkulačce neodmaturovala. Všechny postupy měla dobře, ale číselně měla vše blbě... někdy se zkrátka zadaří... ;)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » imaginární část komplexního čísla (TOTO TÉMA JE VYŘEŠENÉ)

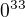 ... ;)
... ;)
 "z hlavy", tak bych si nejdříve určil, kolik je
"z hlavy", tak bych si nejdříve určil, kolik je 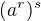 ale nevím co si počnout s "s", když je mocnina lichá..
ale nevím co si počnout s "s", když je mocnina lichá..