Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Základní škola
- » Trojný integrál - válcové souřadnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 06. 2016 02:48
Trojný integrál - válcové souřadnice
Dobrý den,
CHtěl bych se zeptat na příklad na trojitý integrál z válcových souřadnic...
1) jelikož oblast D má několik podmínek, vyjádřil jsem nejprve tu první, x^+y^2 = 4, což je kružnice o polomeru 2. Zakreslil jsem ji!
2) následně, abych dosadil do x^2 + y^2 u rovnice z = 4 - √x^2 + y^2, tak jsem si dosadil souřadnice za x a y, Tedy ϱ^2 * cos^2 φ + ϱ^2 * sin^2 φ = vytknu ϱ^2
-> ϱ^2 * (cos^2 φ + sin^2 φ) = ϱ^2
Dosadil jsem tedy do podmínky u oblasti D, že z = 4 - ϱ, protože odmocnina a ϱ^2 se vyruší, zbyde jen ϱ, tedy 4-ϱ!
CHtěl bych se ale, prosím, zeptat, jak to bude s vybarvením kruhu? Nepoznám z podmínek, jestli bude vybarvená jen nějaká část, a která, nebo jestli celá kružnice?
Podle toho tedy nevím, jak určit souřadnice? ϱ je od 0 do 2. Ovšem φ a z netuším....
A Jak si oblast zakreslit do zetové osy?
Děkuji MNOHOKRÁT ;)
Offline
- (téma jako vyřešené označil(a) DavidMath)
#3 03. 06. 2016 23:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Trojný integrál - válcové souřadnice
Zdravím,
také nevidím žádný důvod, aby byl jen čtvrťkruh (pokud nechybí zápis některé další podmínky). Použila bych celý kruh. Jedině bych překontrolovala, kde se potkají kužel 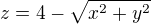 a válec x^2+y^2=4 (nějaký náznak vidím napravo od fialového obdélníku na 2. papíře, ale nejsem si úplně jistá, zda rozumím, jak vzniklo
a válec x^2+y^2=4 (nějaký náznak vidím napravo od fialového obdélníku na 2. papíře, ale nejsem si úplně jistá, zda rozumím, jak vzniklo 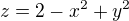 ?
?
A Jak si oblast zakreslit do zetové osy?
provedu svislý řez buď rovinou  nebo rovinou
nebo rovinou  , dosazením jedné nebo druhé této podmínky do
, dosazením jedné nebo druhé této podmínky do 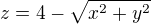 dostanu tvar funkce, kterou zakreslím. Stačí tak? Děkuji.
dostanu tvar funkce, kterou zakreslím. Stačí tak? Děkuji.
Offline
#4 04. 06. 2016 00:15
Re: Trojný integrál - válcové souřadnice
No kamarádka to právě psala v testu a měla tam zaškrtnutou jenom tu čtvrtinu jako mám já, přičemž to neměla škrtlé či opravené, dokonce měla fajfku, že má dobře obrázek a tedy i MEZE u φ!
Jinak 2 - x^ + y^2 jsem dostal tak, že jsem se spletl a má tam být 16 - x^2 + y^2, protože jsem umocnil ten výraz, přičemž mi zmizela odmocnina a 4^2 je 16, je to tak?
Jinak jak by to vypadalo zakreselné v osách tedy?
Děkuji
Offline
#5 04. 06. 2016 08:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Trojný integrál - válcové souřadnice
↑ DavidMath:
potom by musela mít ještě další podmínky. Viděl jsi originální zadání a celý výpočet? Při zadání, jak máš na obrázku, vidím celý kruh, děkuji kolegům, pokud někdo vidí něco jiného.
Jinak 2 - x^ + y^2 jsem dostal tak, že jsem se spletl a má tam být 16 - x^2 + y^2, protože jsem umocnil ten výraz, přičemž mi zmizela odmocnina a 4^2 je 16, je to tak?
:-) to raději neříkej, nebo opět bude přesunuto do ZŠ (provedl jsi krok  , ovšem špatně a nemá být). Postupovala bych spíš tak:
, ovšem špatně a nemá být). Postupovala bych spíš tak: 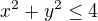 v prostoru určuje válec s podstavou kruh o poloměru 2 jednotky.
v prostoru určuje válec s podstavou kruh o poloměru 2 jednotky. 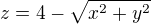 určuje kužel s vrcholem v bodě (0, 0, 4), pro určení podstavy v rovině
určuje kužel s vrcholem v bodě (0, 0, 4), pro určení podstavy v rovině 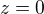 provedu
provedu 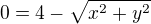 , to mi dá větší podstavný kruh, než podstava válce. Proto musím najít rovnu průsečíku válce a kuželu, která je nad rovinou
, to mi dá větší podstavný kruh, než podstava válce. Proto musím najít rovnu průsečíku válce a kuželu, která je nad rovinou 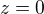 , dosadím do
, dosadím do 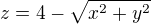 , že
, že 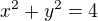 , dostanu, že průsečík je v rovině
, dostanu, že průsečík je v rovině  . Toto je podstatné pro určení poloměru podstavy, zůstává tak, jak jsi určil
. Toto je podstatné pro určení poloměru podstavy, zůstává tak, jak jsi určil 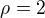 .
.
Jinak jak by to vypadalo zakreselné v osách tedy?
dosazuji do 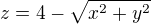 hodnotu x=0 (nebo y=0) (je jasné, proč to dělám?), co vyšlo? Děkuji.
hodnotu x=0 (nebo y=0) (je jasné, proč to dělám?), co vyšlo? Děkuji.
Offline
#6 04. 06. 2016 11:14
Re: Trojný integrál - válcové souřadnice
Našel jsem jeden hodně podobný příklad v sešitě.
Tam učitel vždy vyjadřuje rovnici pro kužel tak, že si za proměnnou, většinou za y, dosazuje 0. Nevím proč taková úprava, ale následně vyšlo to viz vpravu pod nákresem, že pokud je y nula: zbyde 4 - √x^2, tady 4-x
To můžu nakreslit jako přímku 4-x, a platí ti zrcadlově i nadruhou stranu, tedy mám nakreslit automaticky i přímku x+4 ?
Je to jediná úprava, kterou lze provézt, abych zjistil nákres kužele?
Děkuji :) A nezlobte se za mou chybu, spletla mě ta kámoščina verze... 
Offline
#7 04. 06. 2016 11:34 — Editoval DavidMath (04. 06. 2016 11:52) Příspěvek uživatele DavidMath byl skryt uživatelem DavidMath. Důvod: Špatný výsledek
#8 04. 06. 2016 17:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Trojný integrál - válcové souřadnice
↑ DavidMath:
spíš proto, že opět neupravuješ  ještě před integrováním - viz předposlední řádek Tvého scanu - přechod na závěr předposledního (dlouhého) řádku na Tvém scanu je nepěkným důsledkem nedoúprav. Už se v tom, prosím, polepši, děkuji.
ještě před integrováním - viz předposlední řádek Tvého scanu - přechod na závěr předposledního (dlouhého) řádku na Tvém scanu je nepěkným důsledkem nedoúprav. Už se v tom, prosím, polepši, děkuji.
Offline
#9 05. 06. 2016 01:22
Re: Trojný integrál - válcové souřadnice
Prosím, mám dotaz.
Co se týče úprav, jsem se již, doufám, polepšil... Jen mě trápí ten nešťastný sinus, když jej zintegruji, tak - cos!
Vypočítal jsem první i druhý způsob, tedy první s pořadím dz dϱ dφ, kdy to vyšlo kladně, protože je jasné, že uprostřed dané dosazení do - cos, byla nula, ale pokračoval jsem dalším výpočtem dle dϱ, tak to vyšlo kladně, tedy 20.
Pak jsem zkusil integrály dϱ a dφ, protože by měl vyjít stejný výsledek. Chci se zeptat, proč to v tomto případě vychází 0?
Celkově je to velmi zvláštní, protože když dosazuji za - cos, a to 2Pí a 0, tak to vyjde vždy 0, že?
Kde je tedy chyba a v jakém pořadí tedy integrovat?
Děkuji mnohkrát,...
1) 
2) 
Offline
#10 05. 06. 2016 11:44 — Editoval Akojeto (05. 06. 2016 11:50)
- Akojeto
- Příspěvky: 465
Re: Trojný integrál - válcové souřadnice
Ró na druhú krát ró na druhú je ró na štvrtú, nie na tretiu.
Ale neviem, či je to tá príčina, lúštiť sa mi to nechce.
A preboha, píš poriadne zátvorky, nedá sa v tom vyznať.
Ďalej nechápem to +- pred kosínusmi.
Veď kosínus 360 je 1. a. kosínus 0 je 1. Prečo plus mínus?
Offline
#11 05. 06. 2016 11:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Trojný integrál - válcové souřadnice
↑ DavidMath:
v úpravách - důsledně dodržovat závorky, pokud bylo 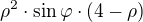 , tak po úpravě musí být
, tak po úpravě musí být 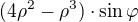 . I přesto, že je vidět, že při výpočtu chybějící závorky "domýšlíš", tak ten zápis musí být správný a bezchybný (ten, kdo kontroluje, nebo jen pročítá Tvé řešení nemá možnost něco domýšlet, když to v zápisu není).
. I přesto, že je vidět, že při výpočtu chybějící závorky "domýšlíš", tak ten zápis musí být správný a bezchybný (ten, kdo kontroluje, nebo jen pročítá Tvé řešení nemá možnost něco domýšlet, když to v zápisu není).
Na 1. scanu v předchozím příspěvku v předposledním řádku vyšlo 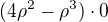 , což je ve výsledku
, což je ve výsledku  , proto integrování jednou a druhou cestou vede k
, proto integrování jednou a druhou cestou vede k  .
.
Jelikož válcové souřadnice převedou kruh v podstavě na obdélník (viz některý teoretický materiál), jedna strana obdélníku jsou meze pro  , druhá strana jsou meze pro
, druhá strana jsou meze pro  , záměnou pořadí těchto 2 proměnných není změna výpočtu a lze provést. Pouze první proměnná, podle které je nutné začínat integrovat, je
, záměnou pořadí těchto 2 proměnných není změna výpočtu a lze provést. Pouze první proměnná, podle které je nutné začínat integrovat, je  (jelikož je funkci prvních 2 proměnných).
(jelikož je funkci prvních 2 proměnných).
K výsledku  - oblast, přes kterou integrujeme, je symetrická ohledně xOz (a yOz), integrujeme sudou funkci (
- oblast, přes kterou integrujeme, je symetrická ohledně xOz (a yOz), integrujeme sudou funkci (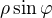 ), výsledek má být nulový. Popř. kontrola WA.
), výsledek má být nulový. Popř. kontrola WA.
V pořádku? Děkuji.
Offline
#12 05. 06. 2016 13:06 — Editoval DavidMath (05. 06. 2016 13:10)
Re: Trojný integrál - válcové souřadnice
Takže pokud vyjde v první možnosti 3 * Integrál 4ϱ^2 - ϱ^3 * [0], je to automaticky nula a už nemusím dále počítat integrál podle ϱ (dϱ)?
Výsledek je prostě 0, i když jsem ještě neintegroval podle ϱ?
Offline
#13 05. 06. 2016 13:27
- misaH
- Příspěvky: 13459
Re: Trojný integrál - válcové souřadnice
↑ DavidMath:
Zas máš blbo zátvorky- prečo to nepíšeš poriadne?
Alebo naozaj myslíš, že to má byť takto?
Ja byť vyučujúci, tak ti to neuznám, lebo v skutočnosti je to zle.![kopírovat do textarea $3 \int 4\rho^2 - \rho^3 \cdot [0]=3\int 4\rho^2-0=3\int4\rho^3$](/mathtex/ed/ed192f364ca2ea184d6ca36dc14ecf6d.gif)
Tak si to už uvedom....
Offline
#14 05. 06. 2016 13:41 — Editoval DavidMath (05. 06. 2016 13:42)
Re: Trojný integrál - válcové souřadnice
↑ misaH:
No a kdybych měl členy naopak tedy že -ϱ^3 + 4ϱ^2 * [0] tak by to opět vyšlo jinak, zbylo by jen -ϱ^3. Takže tomu opravdu nerozumím. Stačí mít naopak členy, což být může a hned je výsledek jinak,...
Protože klidně ty členy mohou být naopak, není to nic co porušuje pravidla a ejhle opět jiný výsledek, podle vašeho postupu.
Nemají být v závorce oba členy zároveň (4ϱ^2 - ϱ^3) * [0] ? = 0. Tedy tak jsem to tedy pochopil od Jeleny, která psala, že to vyjde ta či tak nula. A vy tvrdíte něco jiného.
Nerozumím rozporuplným vysvětlením :) Můžu poprosit o objasnění?
Offline
#15 05. 06. 2016 13:48
Re: Trojný integrál - válcové souřadnice
↑ misaH:
Jo takhle, vy mi ukazujete jak jsem to udělal chybně, a ne, jak to má být. V tom případě ano, ale proto příště prosím dodat, že ukazujete, jak to vypadat nemá, ne tak, že to vypadá jak kdybyste psala správný postup.
děkuji!
Offline
#16 05. 06. 2016 14:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Trojný integrál - válcové souřadnice
Takže pokud vyjde v první možnosti 3 * Integrál 4ϱ^2 - ϱ^3 * [0]
zde pro chybějící závorky 0 nevyjde, nula vyjde tehdy, když závorky důsledně používáš 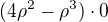 . Pokud je problém si uvědomit - kde závorky ano a kde není nutné, potom přepisuj např. trojné (dvojné) integrály na trojnásobné (dvojnásobné) dle Fubini věty. Tak se Tobě "vnitřní" integrál automaticky dostane do závorek (pokud na závorky dle odkazu nezapomeneš) a už závorky zachováš pro další úpravy.
. Pokud je problém si uvědomit - kde závorky ano a kde není nutné, potom přepisuj např. trojné (dvojné) integrály na trojnásobné (dvojnásobné) dle Fubini věty. Tak se Tobě "vnitřní" integrál automaticky dostane do závorek (pokud na závorky dle odkazu nezapomeneš) a už závorky zachováš pro další úpravy.
Offline
#17 05. 06. 2016 15:11 — Editoval misaH (05. 06. 2016 15:13)
- misaH
- Příspěvky: 13459
Re: Trojný integrál - válcové souřadnice
↑ DavidMath:
Vieš čo - píšem ti, že je to zle a za tým uvádzam tvoj zápis.
A iný výsledok než vyšiel tebe. (Jelena ti o zátvorkách písala niekoľkokrát, tiež zbytočne.)
Podľa mňa to čo som napísala stačí a je to jasné. Nedokážeš si z upozornení brať poučenie.
Z mojej strany už příště nebude, lebo veď načo?
Offline
Stránky: 1
- Hlavní strana
- » Základní škola
- » Trojný integrál - válcové souřadnice (TOTO TÉMA JE VYŘEŠENÉ)

