Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vztahy mezi goniometrickými funkcemi (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 06. 2016 22:57
Vztahy mezi goniometrickými funkcemi
Ahoj, počítal jsem příklady k maturitě (pouze příprava) a narazil jsem na jeden příklad, se kterým si nevím rady.
Zkoušel jsem mnoho způsobů, ale vždy se to nějak "ukončilo".
Díky za pomoc. :-)
Offline
- (téma jako vyřešené označil(a) flagman)
#3 10. 06. 2016 23:34
Re: Vztahy mezi goniometrickými funkcemi
↑ gadgetka:
Ať se snažím, jak se snažím, tak mi to ne a ne vyjít...
Vše jsem dosadil a upravil podle vzorečků a dostal jsem se k tomuto:
Dále jsem pokračoval, ale vyšly mi docela nesmyslné výsledky.
Offline
#4 10. 06. 2016 23:39 — Editoval gadgetka (10. 06. 2016 23:40)
Re: Vztahy mezi goniometrickými funkcemi
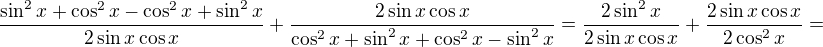

Edit: Špatně jsi upravil jmenovatel druhého zlomku... jinak stačilo krátit zlomky a byl bys u cíle... :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 10. 06. 2016 23:41
Re: Vztahy mezi goniometrickými funkcemi
↑ gadgetka:
Blbá chyba, děkuji. :-)
Už mi to vyšlo. :-)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vztahy mezi goniometrickými funkcemi (TOTO TÉMA JE VYŘEŠENÉ)